Standards Finder
Use this page to find all resources aligned with a particular North Carolina state standard. Simply input the standard, using dot notation, highlight it when it shows up on the drop-down list, and press Apply. You'll see a complete list of all Media4Math resources aligned with that standard.Download your standards report as a CSV file for your reference.To help you with the dot notation, each standard follows this structure.NC.GRADE.STANDARD.BENCHMARKThe table on the right shows the abbreviations for the different standards for K-8. For example, if you are a grade 3 teacher looking for Operations and Algebraic Thinking resources, simply input in the field below "NC.3.OA" and you'll see a drop-down list of possible standards for that grade and topic. Then select the appropriate one and press the Apply button. |
|
| NC Standards | Thumbnail | Title | Description | Curriculum Topic |
|---|---|---|---|---|
| PC.F.7.2 | 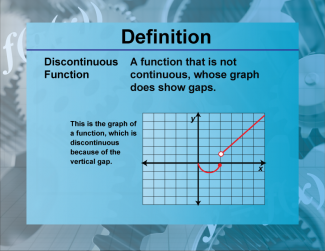
|
Definition--Functions and Relations Concepts--Discontinuous Function |
Definition--Functions and Relations Concepts--Discontinuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Parametric Equations |
Definition--Functions and Relations Concepts--Parametric Equations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 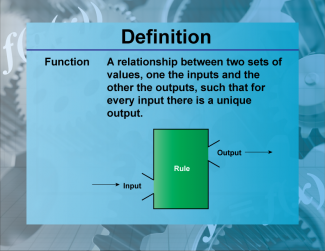
|
Definition--Functions and Relations Concepts--Function |
Definition--Functions and Relations Concepts--Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Discrete Functions |
Definition--Functions and Relations Concepts--Discrete Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.2 | 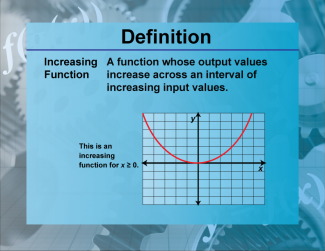
|
Definition--Functions and Relations Concepts--Increasing Function |
Definition--Functions and Relations Concepts--Increasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally |
Definition--Functions and Relations Concepts--Distorting a Function Horizontally
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 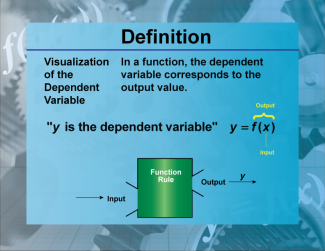
|
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable |
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Graphs of Relations |
Definition--Functions and Relations Concepts--Graphs of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 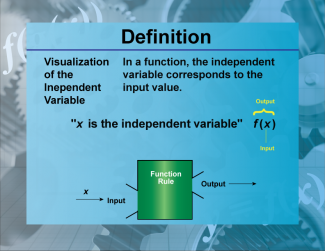
|
Definition--Functions and Relations Concepts--Visualization of the Independent Variable |
Definition--Functions and Relations Concepts--Visualization of the Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Piecewise Functions |
Definition--Functions and Relations Concepts--Piecewise Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.2 | 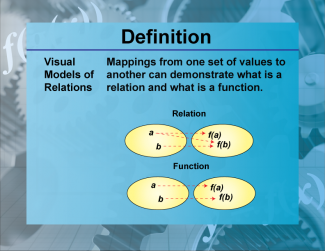
|
Definition--Functions and Relations Concepts--Visual Models of Relations |
Definition--Functions and Relations Concepts--Visual Models of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Absolute Value Function |
Definition--Functions and Relations Concepts--Absolute Value Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Domain of a Function |
Definition--Functions and Relations Concepts--Domain of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Dependent Variable |
Definition--Functions and Relations Concepts--Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Independent Variable |
Definition--Functions and Relations Concepts--Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 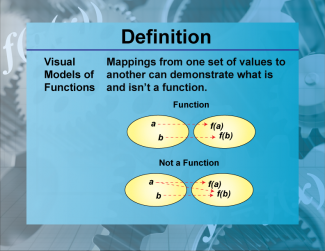
|
Definition--Functions and Relations Concepts--Visual Models of Functions |
Definition--Functions and Relations Concepts--Visual Models of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 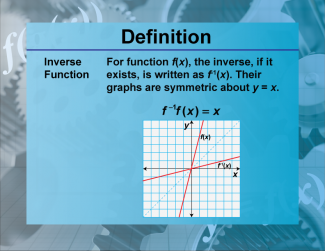
|
Definition--Functions and Relations Concepts--Inverse Function |
Definition--Functions and Relations Concepts--Inverse Function
This is a collection of definitions related to the topic of functions and relations. |
Functions and Their Inverses |
| PC.F.7.2 | 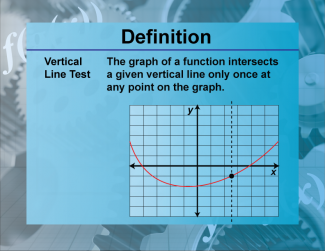
|
Definition--Functions and Relations Concepts--Vertical Line Test |
Definition--Functions and Relations Concepts--Vertical Line Test
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 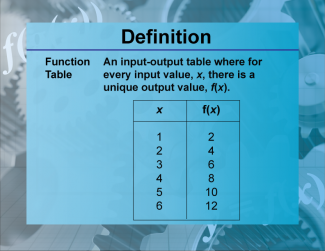
|
Definition--Functions and Relations Concepts--Function Table |
Definition--Functions and Relations Concepts--Function Table
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 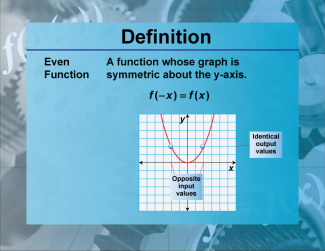
|
Definition--Functions and Relations Concepts--Even Function |
Definition--Functions and Relations Concepts--Even Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Graphs of Functions |
Definition--Functions and Relations Concepts--Graphs of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 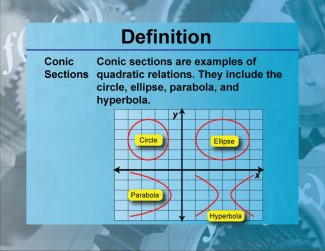
|
Definition--Functions and Relations Concepts--Conic Sections |
Definition--Functions and Relations Concepts--Conic Sections
This is a collection of definitions related to the topic of functions and relations. |
Conic Sections |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Function Notation |
Definition--Functions and Relations Concepts--Function Notation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Reflecting a Function |
Definition--Functions and Relations Concepts--Reflecting a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 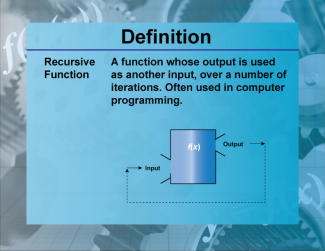
|
Definition--Functions and Relations Concepts--Recursive Function |
Definition--Functions and Relations Concepts--Recursive Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 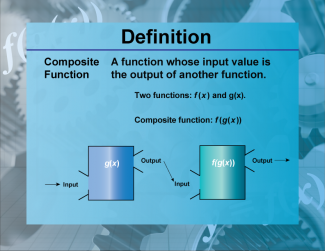
|
Definition--Functions and Relations Concepts--Composite Function |
Definition--Functions and Relations Concepts--Composite Function
Quizlet Flash Cards: Composite FunctionsThis is a collection of definitions related to the topic of functions and relations. |
Composite Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Range of a Function |
Definition--Functions and Relations Concepts--Range of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 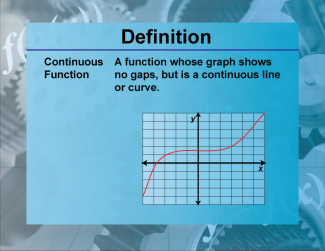
|
Definition--Functions and Relations Concepts--Continuous Function |
Definition--Functions and Relations Concepts--Continuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 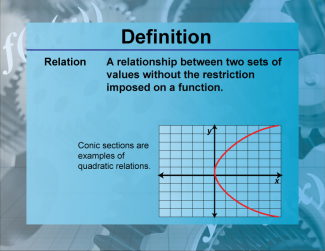
|
Definition--Functions and Relations Concepts--Relation |
Definition--Functions and Relations Concepts--Relation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 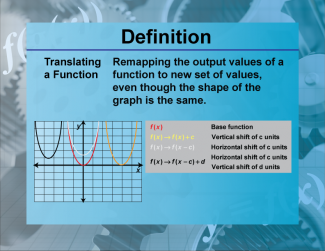
|
Definition--Functions and Relations Concepts--Translating a Function |
Definition--Functions and Relations Concepts--Translating a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 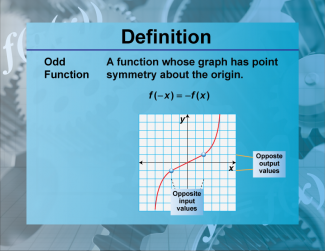
|
Definition--Functions and Relations Concepts--Odd Function |
Definition--Functions and Relations Concepts--Odd Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 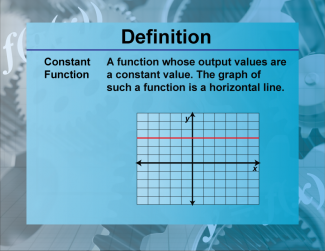
|
Definition--Functions and Relations Concepts--Constant Function |
Definition--Functions and Relations Concepts--Constant Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Vertically |
Definition--Functions and Relations Concepts--Distorting a Function Vertically
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 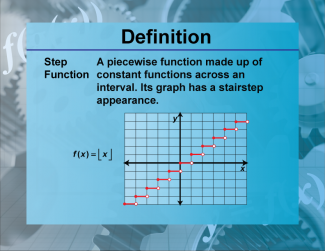
|
Definition--Functions and Relations Concepts--Step Function |
Definition--Functions and Relations Concepts--Step Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.2 | 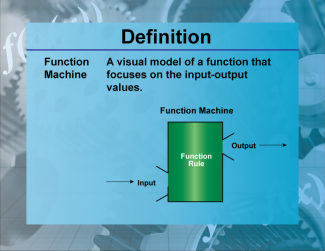
|
Definition--Functions and Relations Concepts--Function Machine |
Definition--Functions and Relations Concepts--Function Machine
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.2 | 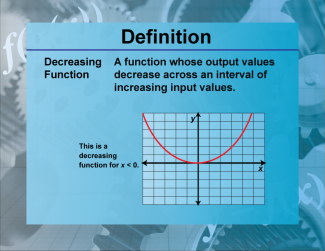
|
Definition--Functions and Relations Concepts--Decreasing Function |
Definition--Functions and Relations Concepts--Decreasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Visual Models of Functions |
Definition--Functions and Relations Concepts--Visual Models of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Conic Sections |
Definition--Functions and Relations Concepts--Conic Sections
This is a collection of definitions related to the topic of functions and relations. |
Conic Sections |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Vertically |
Definition--Functions and Relations Concepts--Distorting a Function Vertically
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Composite Function |
Definition--Functions and Relations Concepts--Composite Function
Quizlet Flash Cards: Composite FunctionsThis is a collection of definitions related to the topic of functions and relations. |
Composite Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Graphs of Functions |
Definition--Functions and Relations Concepts--Graphs of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Discontinuous Function |
Definition--Functions and Relations Concepts--Discontinuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Function Table |
Definition--Functions and Relations Concepts--Function Table
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Piecewise Functions |
Definition--Functions and Relations Concepts--Piecewise Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Decreasing Function |
Definition--Functions and Relations Concepts--Decreasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Vertical Line Test |
Definition--Functions and Relations Concepts--Vertical Line Test
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Visualization of the Independent Variable |
Definition--Functions and Relations Concepts--Visualization of the Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Function Notation |
Definition--Functions and Relations Concepts--Function Notation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Continuous Function |
Definition--Functions and Relations Concepts--Continuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Inverse Function |
Definition--Functions and Relations Concepts--Inverse Function
This is a collection of definitions related to the topic of functions and relations. |
Functions and Their Inverses |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Absolute Value Function |
Definition--Functions and Relations Concepts--Absolute Value Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Graphs of Relations |
Definition--Functions and Relations Concepts--Graphs of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Translating a Function |
Definition--Functions and Relations Concepts--Translating a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Function |
Definition--Functions and Relations Concepts--Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Visual Models of Relations |
Definition--Functions and Relations Concepts--Visual Models of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Recursive Function |
Definition--Functions and Relations Concepts--Recursive Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Relation |
Definition--Functions and Relations Concepts--Relation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Step Function |
Definition--Functions and Relations Concepts--Step Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Reflecting a Function |
Definition--Functions and Relations Concepts--Reflecting a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Increasing Function |
Definition--Functions and Relations Concepts--Increasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Parametric Equations |
Definition--Functions and Relations Concepts--Parametric Equations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Dependent Variable |
Definition--Functions and Relations Concepts--Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Discrete Functions |
Definition--Functions and Relations Concepts--Discrete Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Even Function |
Definition--Functions and Relations Concepts--Even Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Independent Variable |
Definition--Functions and Relations Concepts--Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally |
Definition--Functions and Relations Concepts--Distorting a Function Horizontally
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Function Machine |
Definition--Functions and Relations Concepts--Function Machine
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Range of a Function |
Definition--Functions and Relations Concepts--Range of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable |
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Odd Function |
Definition--Functions and Relations Concepts--Odd Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Constant Function |
Definition--Functions and Relations Concepts--Constant Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7.1 | 
|
Definition--Functions and Relations Concepts--Domain of a Function |
Definition--Functions and Relations Concepts--Domain of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Increasing Function |
Definition--Functions and Relations Concepts--Increasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Graphs of Functions |
Definition--Functions and Relations Concepts--Graphs of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Visual Models of Relations |
Definition--Functions and Relations Concepts--Visual Models of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Range of a Function |
Definition--Functions and Relations Concepts--Range of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Odd Function |
Definition--Functions and Relations Concepts--Odd Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Function |
Definition--Functions and Relations Concepts--Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Discontinuous Function |
Definition--Functions and Relations Concepts--Discontinuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Decreasing Function |
Definition--Functions and Relations Concepts--Decreasing Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Function Machine |
Definition--Functions and Relations Concepts--Function Machine
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Function Notation |
Definition--Functions and Relations Concepts--Function Notation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Piecewise Functions |
Definition--Functions and Relations Concepts--Piecewise Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Continuous Function |
Definition--Functions and Relations Concepts--Continuous Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Independent Variable |
Definition--Functions and Relations Concepts--Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Inverse Function |
Definition--Functions and Relations Concepts--Inverse Function
This is a collection of definitions related to the topic of functions and relations. |
Functions and Their Inverses |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Visualization of the Independent Variable |
Definition--Functions and Relations Concepts--Visualization of the Independent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Composite Function |
Definition--Functions and Relations Concepts--Composite Function
Quizlet Flash Cards: Composite FunctionsThis is a collection of definitions related to the topic of functions and relations. |
Composite Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Reflecting a Function |
Definition--Functions and Relations Concepts--Reflecting a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Step Function |
Definition--Functions and Relations Concepts--Step Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable |
Definition--Functions and Relations Concepts--Visualization of the Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Function Table |
Definition--Functions and Relations Concepts--Function Table
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Visual Models of Functions |
Definition--Functions and Relations Concepts--Visual Models of Functions
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Horizontally |
Definition--Functions and Relations Concepts--Distorting a Function Horizontally
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Relation |
Definition--Functions and Relations Concepts--Relation
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Recursive Function |
Definition--Functions and Relations Concepts--Recursive Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Absolute Value Function |
Definition--Functions and Relations Concepts--Absolute Value Function
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Even Function |
Definition--Functions and Relations Concepts--Even Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Graphs of Relations |
Definition--Functions and Relations Concepts--Graphs of Relations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Dependent Variable |
Definition--Functions and Relations Concepts--Dependent Variable
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Conic Sections |
Definition--Functions and Relations Concepts--Conic Sections
This is a collection of definitions related to the topic of functions and relations. |
Conic Sections |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Constant Function |
Definition--Functions and Relations Concepts--Constant Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Vertical Line Test |
Definition--Functions and Relations Concepts--Vertical Line Test
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Distorting a Function Vertically |
Definition--Functions and Relations Concepts--Distorting a Function Vertically
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Discrete Functions |
Definition--Functions and Relations Concepts--Discrete Functions
This is a collection of definitions related to the topic of functions and relations. |
Special Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Translating a Function |
Definition--Functions and Relations Concepts--Translating a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Parametric Equations |
Definition--Functions and Relations Concepts--Parametric Equations
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.7 | 
|
Definition--Functions and Relations Concepts--Domain of a Function |
Definition--Functions and Relations Concepts--Domain of a Function
This is a collection of definitions related to the topic of functions and relations. |
Relations and Functions |
| PC.F.6.2 | 
|
Instructional Resource Collection: The Fibonacci Sequence |
This is a collection of lessons on the Fibonacci Sequence. There are six lessons. | Sequences, Exploring Coordinate Systems, Applications of Exponential and Logarithmic Functions, Ratios and Rates, Proportions, Geometric Constructions with Triangles and Applications of Quadrilaterals |
| PC.F.6.2 | 
|
Math Examples Collection: Explicit and Recursive Formulas |
This collection aggregates all the math examples around the topic of Explicit and Recursive Formulas. There are a total of 50 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans. | Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 4 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 4
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 9 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 9
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 6 |
Instructional Resource | Fibonacci Sequence, Lesson 6
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at geometric constructions that reflect the golden ratio. |
Sequences, Geometric Constructions with Triangles and Applications of Quadrilaterals |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 7 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 7
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 4 |
Instructional Resource | Fibonacci Sequence, Lesson 4
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the Golden Ratio phi. |
Sequences, Ratios and Rates and Proportions |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 10 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 10
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 6 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 6
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 4 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 4
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 7 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 7
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 8 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 8
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 1 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 1
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 2 |
Instructional Resource | Fibonacci Sequence, Lesson 2
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the sequence as an example of a recursive function. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 5 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 5
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 2 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 2
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 8 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 8
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 2 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 2
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 6 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 6
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 9 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 9
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 1 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 1
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 5 |
Instructional Resource | Fibonacci Sequence, Lesson 5
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the Golden Ratio phi. |
Sequences, Ratios and Rates and Proportions |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 7 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 7
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 5 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 5
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 3 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 3
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 3 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 3
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 9 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 9
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 6 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 6
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 1 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 1
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 7 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 7
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 4 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 4
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 8 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 8
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 1 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 1
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 3 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 3
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 2 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 2
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 2 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 2
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 6 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 6
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 8 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 8
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 3 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 3
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 1 |
Instructional Resource | Fibonacci Sequence, Lesson 1
The year 2023 is the Year of the Rabbit in the Chinese Zodiac. Media4Math would also like to make this the Year of Fibonacci. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 10 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 10
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Instructional Resource--Fibonacci Sequence, Lesson 3 |
Instructional Resource | Fibonacci Sequence, Lesson 3
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the sequence as a logarithmic spiral. |
Exploring Coordinate Systems and Applications of Exponential and Logarithmic Functions |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 4 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 4
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 10 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 10
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 9 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 9
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 2 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 2
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 5 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 5
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 6 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 6
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 9 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 9
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 5 |
Math Example--Sequences and Series--Finding the Explicit Formula of an Arithmetic Sequence: Example 5
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 5 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 5
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 4 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 4
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 10 |
Math Example--Sequences and Series--Finding the Explicit Formula of a Geometric Sequence: Example 10
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 8 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 8
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 1 |
Math Example--Sequences and Series--Finding the Recursive Formula of an Arithmetic Sequence: Example 1
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 7 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 7
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 3 |
Math Example--Sequences and Series--Finding the nth Term of an Arithmetic Sequence: Example 3
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.2 | 
|
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 10 |
Math Example--Sequences and Series--Finding the Recursive Formula of a Geometric Sequence: Example 10
This is part of a collection of math examples that focus on sequences and series. |
Sequences |
| PC.F.6.1 | 
|
Math Video Collection: Texas Instruments Tutorial Videos |
This collection aggregates all the math videos and resources in this series: Texas Instruments Tutorial Videos. There are a total of 266 resources. | Rational Expressions, Sequences, Series, Polynomial Functions and Equations, Graphs of Quadratic Functions, Quadratic Equations and Functions, Solving Systems of Equations, Trig Expressions and Identities, Probability, Geometric Constructions with Triangles, Composite Functions, Geometric Constructions with Angles and Planes, Distance Formula, Data Analysis, Slope, Special Functions, Trigonometric Functions, Graphs of Exponential and Logarithmic Functions, Radical Functions and Equations, Rational Functions and Equations, Slope-Intercept Form, Coordinate Systems, Graphs of Linear Functions, Inequalities, Matrix Operations and Midpoint Formula |
| PC.F.6.1 | 
|
Closed Captioned Video: Exp induction 1 |
Closed Captioned Video: Exp induction 1
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum of sequence of consecutive integers, as well as deriving the general formu |
Sequences and Series |
| PC.F.6.1 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers |
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Exploring ind |
Sequences and Series |
| PC.F.6.1 | 
|
Closed Captioned Video: Exp induction 2 |
Closed Captioned Video: Exp induction 2
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum of sequence of consecutive odd integers, as well as deriving the general f |
Sequences and Series |
| PC.F.6.1 | 
|
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers |
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
This is part of a collection of math worksheets on the use of the TI-Nspire graphing calc |
Sequences and Series |
| PC.F.6.1 | 
|
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers |
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
This is part of a collection of math worksheets on the use of the TI-Nspire graphing |
Sequences and Series |
| PC.F.6.1 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 25 |
VIDEO: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum |
Sequences and Series |
| PC.F.6.1 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 26 |
VIDEO: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the |
Sequences and Series |
| PC.F.6.1 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers |
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Exploring inducti |
Sequences and Series |
| PC.F.6 | 
|
Math Video Collection: Texas Instruments Tutorial Videos |
This collection aggregates all the math videos and resources in this series: Texas Instruments Tutorial Videos. There are a total of 266 resources. | Rational Expressions, Sequences, Series, Polynomial Functions and Equations, Graphs of Quadratic Functions, Quadratic Equations and Functions, Solving Systems of Equations, Trig Expressions and Identities, Probability, Geometric Constructions with Triangles, Composite Functions, Geometric Constructions with Angles and Planes, Distance Formula, Data Analysis, Slope, Special Functions, Trigonometric Functions, Graphs of Exponential and Logarithmic Functions, Radical Functions and Equations, Rational Functions and Equations, Slope-Intercept Form, Coordinate Systems, Graphs of Linear Functions, Inequalities, Matrix Operations and Midpoint Formula |
| PC.F.6 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers |
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Exploring ind |
Sequences and Series |
| PC.F.6 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 25 |
VIDEO: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum |
Sequences and Series |
| PC.F.6 | 
|
Closed Captioned Video: Exp induction 1 |
Closed Captioned Video: Exp induction 1
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum of sequence of consecutive integers, as well as deriving the general formu |
Sequences and Series |
| PC.F.6 | 
|
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers |
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
This is part of a collection of math worksheets on the use of the TI-Nspire graphing calc |
Sequences and Series |
| PC.F.6 | 
|
Closed Captioned Video: Exp induction 2 |
Closed Captioned Video: Exp induction 2
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the sum of sequence of consecutive odd integers, as well as deriving the general f |
Sequences and Series |
| PC.F.6 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers |
Video Transcript: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Integers
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Exploring inducti |
Sequences and Series |
| PC.F.6 | 
|
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers |
Worksheet: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
This is part of a collection of math worksheets on the use of the TI-Nspire graphing |
Sequences and Series |
| PC.F.6 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 26 |
VIDEO: TI-Nspire Mini-Tutorial: (CAS) Exploring induction: Finding the Formula for the Sum of Consecutive Odd Integers
In this TI Nspire tutorial for the TI-Nspire CAS, the Graphing window is used to find the |
Sequences and Series |
| PC.F.5.7 | 
|
Math Definitions Collection--Calculus Concepts |
This collection aggregates all the definitions for key terms in a standards Calculus course. There are a total of 88 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. | Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Differentiation |
Definition--Calculus Topics--Differentiation
The process of finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.7 | 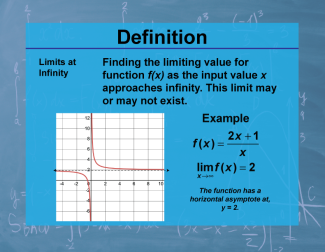
|
Definition--Calculus Topics--Limits at Infinity |
Definition--Calculus Topics--Limits at Infinity
Finding the limiting value for function f(x) as the input value x approaches infinity. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Polynomial Function |
Definition--Calculus Topics--Derivative of a Polynomial Function
The derivative of a polynomial of degree n is another polynomial of degree n - 1. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Indefinite Integral |
Definition--Calculus Topics--Indefinite Integral
The integral of a function without a specific limit on the endpoints. The result of an indefinite integral is a differentiable function. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Logarithmic Function |
Definition--Calculus Topics--Derivative of a Logarithmic Function
The derivative of a logarithmic function uses the laws of logarithms and the definition of e to find the derivative. |
Calculus Vocabulary |
| PC.F.5.7 | 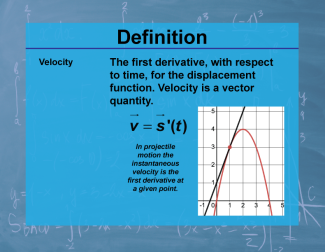
|
Definition--Calculus Topics--Velocity |
Definition--Calculus Topics--Velocity
The first derivative, with respect to time, for the displacement function. Velocity is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Composite Function |
Definition--Calculus Topics--Derivative of a Composite Function
For two functions f(x) and g(x), the derivative of the composite function f(g(x)) is f'(x)*g'(x). This is an example of the Chain Rule. |
Calculus Vocabulary |
| PC.F.5.7 | 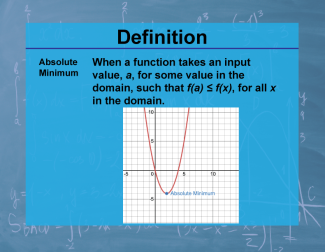
|
Definition--Calculus Topics--Absolute Minimum |
Definition--Calculus Topics--Absolute Minimum
When a function takes an input value, a, for some value in the domain, such that f(a) ≤ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.7 | 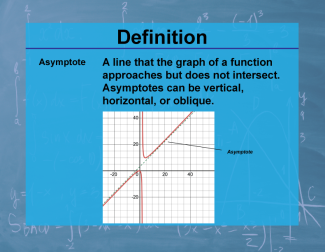
|
Definition--Calculus Topics--Asymptote |
Definition--Calculus Topics--Asymptote
A line that the graph of a function approaches but does not intersect. Asymptotes can be vertical, horizontal, or oblique. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Area Beneath a Curve |
Definition--Calculus Topics--Area Beneath a Curve
For a definite integral, it is the numerical result of the integration. |
Calculus Vocabulary |
| PC.F.5.7 | 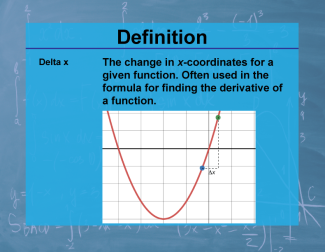
|
Definition--Calculus Topics--Delta x |
Definition--Calculus Topics--Delta x
The change in x-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Power Rule |
Definition--Calculus Topics--Power Rule
The process of finding the derivative of a power function. |
Calculus Vocabulary |
| PC.F.5.7 | 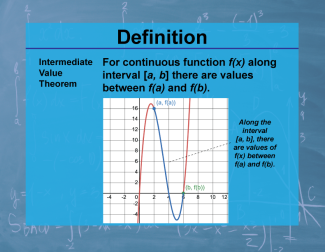
|
Definition--Calculus Topics--Intermediate Value Theorem |
Definition--Calculus Topics--Intermediate Value Theorem
For continuous function f(x) along interval [a, b] there are values between f(a) and f(b). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Antiderivative |
Definition--Calculus Topics--Antiderivative
For two differentiable functions f(x) and F(x), if F'(x) = f(x), then F(x) is the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Explicit Function |
Definition--Calculus Topics--Explicit Function
A function in which y can be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equation. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Composite Function |
Definition--Calculus Topics--Composite Function
A function whose input values are made up of another function. For two functions f(x) and g(x), a composite function can be written as f(g(x)). |
Calculus Vocabulary |
| PC.F.5.7 | 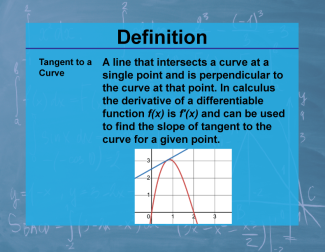
|
Definition--Calculus Topics--Tangent to a Curve |
Definition--Calculus Topics--Tangent to a Curve
A line that intersects a curve at a single point and is perpendicular to the curve at that point. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Fundamental Theorem of Calculus |
Definition--Calculus Topics--Fundamental Theorem of Calculus
The theorem that relates differentiation and integration. The two operations are basically inverses of each other. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--L'Hopital's Rule |
Definition--Calculus Topics--L'Hopital's Rule
For function f(x)/g(x), where f(x) and g(x) are two functions, along an interval [a, b], if there is a point c in the interval such that g(x) = 0, then L'Hopital' |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Acceleration |
Definition--Calculus Topics--Acceleration
The second derivative, with respect to time, for the displacement function. Acceleration is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Definite Integral |
Definition--Calculus Topics--Definite Integral
The integral of a function with specific limits on the endpoints. A definite integral results in a numerical value. |
Calculus Vocabulary |
| PC.F.5.7 | 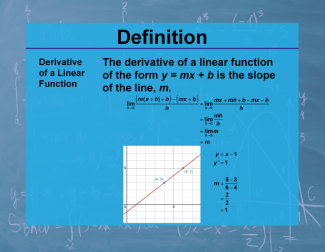
|
Definition--Calculus Topics--Derivative of a Linear Function |
Definition--Calculus Topics--Derivative of a Linear Function
The derivative of a linear function of the form y = mx + b is the slope of the line, m. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function |
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function
Use implicit differentiation and the quotient rule to find the derivative of an inverse trig function. |
Calculus Vocabulary |
| PC.F.5.7 | 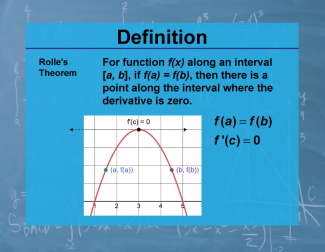
|
Definition--Calculus Topics--Rolle's Theorem |
Definition--Calculus Topics--Rolle's Theorem
For function f(x) along an interval [a, b], if f(a) = f(b), then there is a point along the interval where the derivative is zero. |
Calculus Vocabulary |
| PC.F.5.7 | 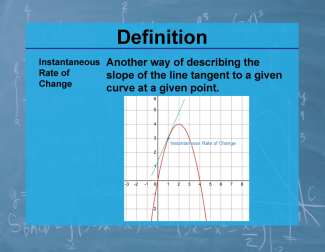
|
Definition--Calculus Topics--Instantaneous Rate of Change |
Definition--Calculus Topics--Instantaneous Rate of Change
Another way of describing the slope of the line tangent to a given curve at a given point. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Step Function |
Definition--Calculus Topics--Step Function
A discontinuous function whose graph looks like a staircase. A step function can be generated by ceiling or floor functions. |
Calculus Vocabulary |
| PC.F.5.7 | 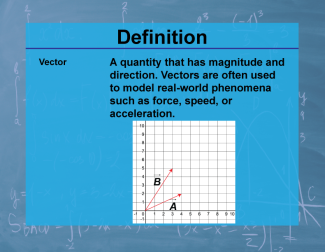
|
Definition--Calculus Topics--Vector |
Definition--Calculus Topics--Vector
A quantity that has magnitude and direction. Vectors are often used to model real-world phenomena such as force, speed, or acceleration. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Parametric Equations |
Definition--Calculus Topics--Parametric Equations
A set of equations where each variable, x and y, is a function of a third variable, t. Graphs of parametric equations are sometimes not functions. |
Calculus Vocabulary |
| PC.F.5.7 | 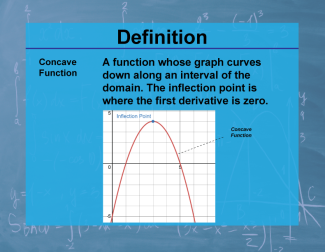
|
Definition--Calculus Topics--Concave Function |
Definition--Calculus Topics--Concave Function
A function whose graph curves down along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.7 | 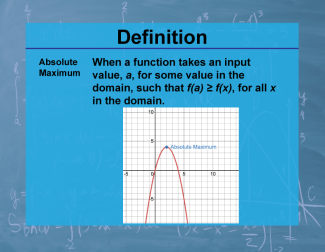
|
Definition--Calculus Topics--Absolute Maximum |
Definition--Calculus Topics--Absolute Maximum
When a function takes an input value, a, for some value in the domain, such that f(a) ≥ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Local Maximum |
Definition--Calculus Topics--Local Maximum
When a function takes an input value, a, for some region in the domain, such that f(a) ≥ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.7 | 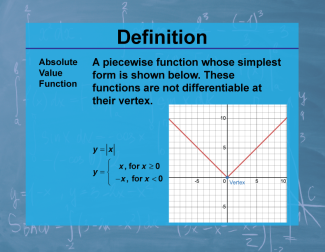
|
Definition--Calculus Topics--Absolute Value Function |
Definition--Calculus Topics--Absolute Value Function
A piecewise function whose simplest form is shown below. These functions are not differentiable at their vertex. |
Calculus Vocabulary |
| PC.F.5.7 | 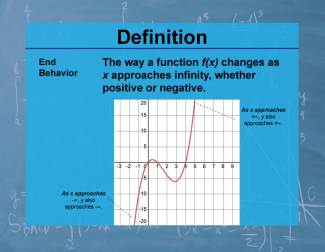
|
Definition--Calculus Topics--End Behavior |
Definition--Calculus Topics--End Behavior
The way a function f(x) changes as x approaches infinity, whether positive or negative. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Trig Function |
Definition--Calculus Topics--Derivative of a Trig Function
The derivative of a trig function is another trig function, as shown in the table. |
Calculus Vocabulary |
| PC.F.5.7 | 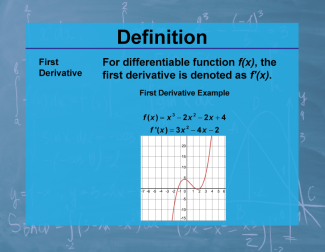
|
Definition--Calculus Topics--First Derivative |
Definition--Calculus Topics--First Derivative
For differentiable function f(x), the first derivative is denoted as f'(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Limit |
Definition--Calculus Topics--Limit
As a function f(x) approaches a specific input value a, the function may approach a specific limiting value. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Local Minimum |
Definition--Calculus Topics--Local Minimum
When a function takes an input value, a, for some region in the domain, such that f(a) ≤ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of an Exponential Function |
Definition--Calculus Topics--Derivative of an Exponential Function
The derivative of an exponential function is the product of the function and the natural log of the base. The derivative of ex is ex. |
Calculus Vocabulary |
| PC.F.5.7 | 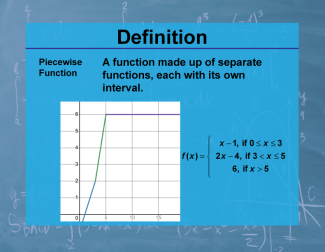
|
Definition--Calculus Topics--Piecewise Function |
Definition--Calculus Topics--Piecewise Function
A function made up of separate functions, each with its own interval. |
Calculus Vocabulary |
| PC.F.5.7 | 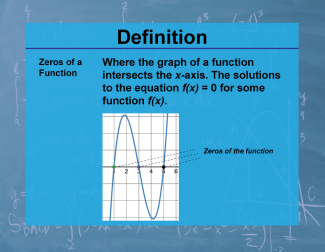
|
Definition--Calculus Topics--Zeros of a Function |
Definition--Calculus Topics--Zeros of a Function
Where the graph of a function intersects the x-axis. The solutions to the equation f(x) = 0 for some function f(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Power Function |
Definition--Calculus Topics--Power Function
A function with a single term that consists of a variable base raised to a real number power. The variable can also have a real number coefficient. |
Calculus Vocabulary |
| PC.F.5.7 | 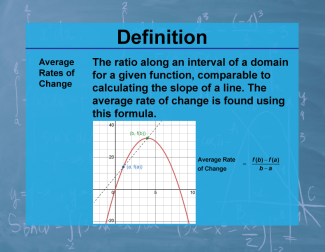
|
Definition--Calculus Topics--Average Rates of Change |
Definition--Calculus Topics--Average Rates of Change
The ratio along an interval of a domain for a given function, comparable to calculating the slope of a line. |
Calculus Vocabulary |
| PC.F.5.7 | 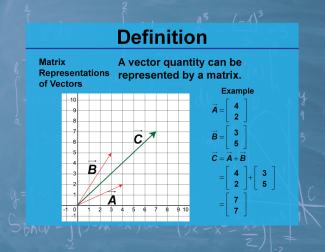
|
Definition--Calculus Topics--Matrix Representations of Vectors |
Definition--Calculus Topics--Matrix Representations of Vectors
A vector quantity can be represented by a matrix. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Sigma Notation |
Definition--Calculus Topics--Sigma Notation
The Greek letter used for summarizing terms of a finite or infinite sequence. |
Calculus Vocabulary |
| PC.F.5.7 | 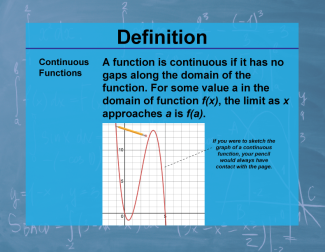
|
Definition--Calculus Topics--Continuous Functions |
Definition--Calculus Topics--Continuous Functions
A function is continuous if it has no gaps along the domain of the function. |
Calculus Vocabulary |
| PC.F.5.7 | 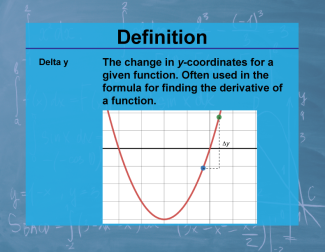
|
Definition--Calculus Topics--Delta y |
Definition--Calculus Topics--Delta y
The change in y-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.7 | 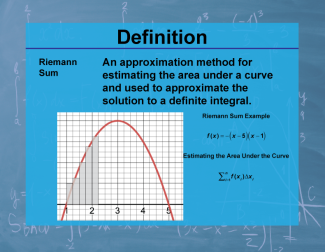
|
Definition--Calculus Topics--Riemann Sum |
Definition--Calculus Topics--Riemann Sum
An approximation method for estimating the area under a curve and used to approximate the solution to a definite integral. |
Calculus Vocabulary |
| PC.F.5.7 | 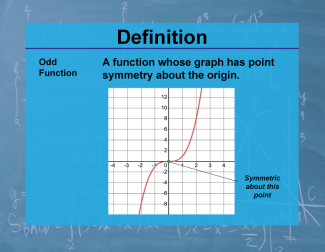
|
Definition--Calculus Topics--Odd Function |
Definition--Calculus Topics--Odd Function
A function whose graph has point symmetry about the origin. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Integrand |
Definition--Calculus Topics--Integrand
In the process of integration, it is the function that is being integrated. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Displacement Function |
Definition--Calculus Topics--Displacement Function
A distance-vs.-time function used to find the distance an object has moved from a starting point. |
Calculus Vocabulary |
| PC.F.5.7 | 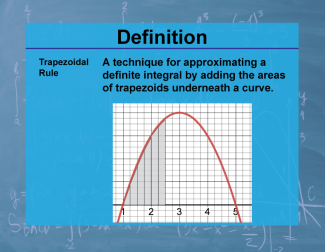
|
Definition--Calculus Topics--Trapezoidal Rule |
Definition--Calculus Topics--Trapezoidal Rule
A technique for approximating a definite integral by adding the areas of trapezoids underneath a curve. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Rational Function |
Definition--Calculus Topics--Derivative of a Rational Function
Since a rational function is the ratio of two polynomials, the derivative of a rational function is also the ratio of two polynomials. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Sum Rule |
Definition--Calculus Topics--Sum Rule
For differentiable functions f(x) and g(x) along a given interval, the derivative of the sum f(x) + g(x) is the sum of the individual derivatives f'(x) and g'(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Floor Function |
Definition--Calculus Topics--Floor Function
A discrete function that takes real number values and whose output is the greatest integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Integral Symbol |
Definition--Calculus Topics--Integral Symbol
The mathematical symbol used to denote the process of integration. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative |
Definition--Calculus Topics--Derivative
A function used to find the slope of a tangent to a curve at a given point. The derivative is based on the following limit. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Implicit Function |
Definition--Calculus Topics--Implicit Function
A function in which y cannot be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equatio |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Change of Variables |
Definition--Calculus Topics--Change of Variables
A substitution technique where a variable replaces a more complicated expression. In calculus it can simplify differentiation or integration. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Hooke's Law |
Definition--Calculus Topics--Hooke's Law
A second-order differential equation that is used to model simple harmonic motion using a trigonometric function. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Differential Equation |
Definition--Calculus Topics--Differential Equation
An equation that includes the derivative of a function f(x) and the variable x. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Discrete Function |
Definition--Calculus Topics--Discrete Function
A function whose graphs has gaps. This is because the function consists of separate ordered pairs or is a discontinuous function with gaps. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Inverse Function |
Definition--Calculus Topics--Inverse Function
For function f(x), the inverse function f-1(x), if it exists, undoes the mapping of the original function. |
Calculus Vocabulary |
| PC.F.5.7 | 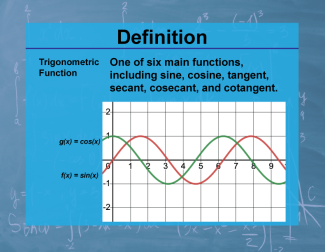
|
Definition--Calculus Topics--Trigonometric Function |
Definition--Calculus Topics--Trigonometric Function
One of six main functions, including sine, cosine, tangent, secant, cosecant, and cotangent. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Ceiling Function |
Definition--Calculus Topics--Ceiling Function
A discrete function that takes real number values and whose output is the least integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Integration by Substitution |
Definition--Calculus Topics--Integration by Substitution
Replacing the integrand with a simpler expression to make the process of integration easier. |
Calculus Vocabulary |
| PC.F.5.7 | 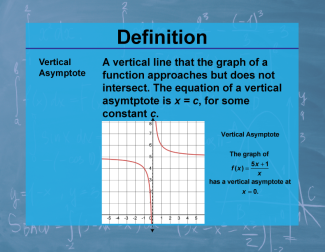
|
Definition--Calculus Topics--Vertical Asymptote |
Definition--Calculus Topics--Vertical Asymptote
A vertical line that the graph of a function approaches but does not intersect. The equation of a vertical asymptote is x = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Separable Differential Equation |
Definition--Calculus Topics--Separable Differential Equation
A special type of differential equation in which functions f(x) and g(y) can be separated to find the solution to the equation. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Linear Approximation |
Definition--Calculus Topics--Linear Approximation
For differentiable function f(x), the linear approximation at x = a, for some real number a, is the equation of the line tangent to f(x) at a. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Integral |
Definition--Calculus Topics--Integral
A method for finding the area of a curve along an interval. In calculus, integrating a function f(x) involves finding the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Derivative of a Quadratic Function |
Definition--Calculus Topics--Derivative of a Quadratic Function
Since a quadratic function is a polynomial function of degree 2, the derivative is a linear function. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Chain Rule |
Definition--Calculus Topics--Chain Rule
The process for finding the derivative of a composite function. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Implicit Differentiation |
Definition--Calculus Topics--Implicit Differentiation
When a function cannot be written in the form of y as a function of x, then implicit differentation can be used to find the derivative with respect to x. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Quotient Rule |
Definition--Calculus Topics--Quotient Rule
The rule for finding the derivative of a function made up of the ratios of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Inflection Point |
Definition--Calculus Topics--Inflection Point
The point on a curve where the curvature changes. This is often indicated by a change in the slopes of tangents to the curve. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Mean Value Theorem |
Definition--Calculus Topics--Mean Value Theorem
For differentiable function f(x) along the closed interval [a, b] there is a value c within that interval such that f'(c) is parallel to the secant formed by th |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Rational Function |
Definition--Calculus Topics--Rational Function
A function made up of the ratio of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.7 | 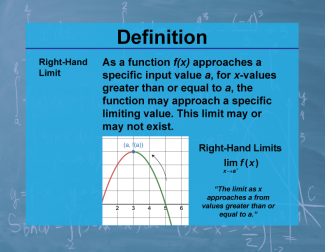
|
Definition--Calculus Topics--Right-Hand Limit |
Definition--Calculus Topics--Right-Hand Limit
As a function f(x) approaches a specific input value a, for x-values greater than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.7 | 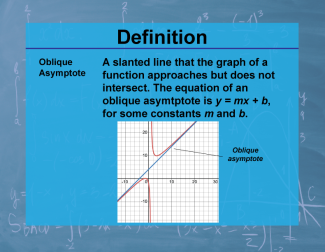
|
Definition--Calculus Topics--Oblique Asymptote |
Definition--Calculus Topics--Oblique Asymptote
A slanted line that the graph of a function approaches but does not intersect. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Differentiable Function |
Definition--Calculus Topics--Differentiable Function
A function is differentiable if a derivative can be found at each point in its domain. |
Calculus Vocabulary |
| PC.F.5.7 | 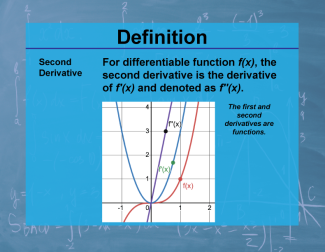
|
Definition--Calculus Topics--Second Derivative |
Definition--Calculus Topics--Second Derivative
For differentiable function f(x), the second derivative is the derivative of f'(x) and denoted as f''(x). |
Calculus Vocabulary |
| PC.F.5.7 | 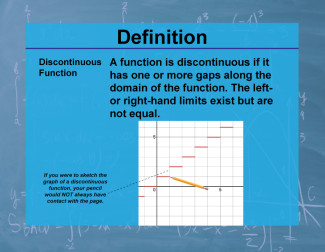
|
Definition--Calculus Topics--Discontinuous Function |
Definition--Calculus Topics--Discontinuous Function
A function is discontinuous if it has one or more gaps along the domain of the function. The left- or right-hand limits exist but are not equal. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Trig Identities |
Definition--Calculus Topics--Trig Identities
Equations that involve trigonmetric functions and are often used to simplify certain trigonometric expressions. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--One-Sided Limits |
Definition--Calculus Topics--One-Sided Limits
Restricting the limit of a function for values approaching the limiting value from one side. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Extreme Value Theorem |
Definition--Calculus Topics--Extreme Value Theorem
For function f(x) along an interval, there are maximum and minimum values. If the derivative is zero along this interval, this is an inflection point. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Horizontal Asymptote |
Definition--Calculus Topics--Horizontal Asymptote
A horizontal line that the graph of a function approaches but does not intersect. The equation of a horizontal asymptote is y = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.7 | 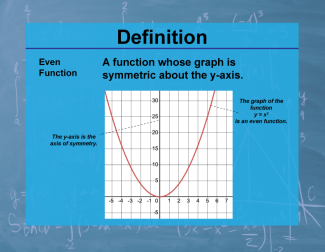
|
Definition--Calculus Topics--Even Function |
Definition--Calculus Topics--Even Function
A function whose graph is symmetric about the y-axis. |
Calculus Vocabulary |
| PC.F.5.7 | 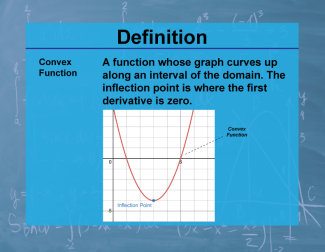
|
Definition--Calculus Topics--Convex Function |
Definition--Calculus Topics--Convex Function
A function whose graph curves up along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.7 | 
|
Definition--Calculus Topics--Left-Hand Limit |
Definition--Calculus Topics--Left-Hand Limit
As a function f(x) approaches a specific input value a, for x-values less than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.6 | 
|
INSTRUCTIONAL RESOURCE: Math Examples 18 |
INSTRUCTIONAL RESOURCE: Math Examples--Functions and Their Inverses
This set of tutorials provides 18 examples that explore the concept of functions and their inverses. |
Functions and Their Inverses |
| PC.F.5.5 | 
|
Math Definitions Collection--Calculus Concepts |
This collection aggregates all the definitions for key terms in a standards Calculus course. There are a total of 88 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. | Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Tangent to a Curve |
Definition--Calculus Topics--Tangent to a Curve
A line that intersects a curve at a single point and is perpendicular to the curve at that point. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Mean Value Theorem |
Definition--Calculus Topics--Mean Value Theorem
For differentiable function f(x) along the closed interval [a, b] there is a value c within that interval such that f'(c) is parallel to the secant formed by th |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Left-Hand Limit |
Definition--Calculus Topics--Left-Hand Limit
As a function f(x) approaches a specific input value a, for x-values less than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Instantaneous Rate of Change |
Definition--Calculus Topics--Instantaneous Rate of Change
Another way of describing the slope of the line tangent to a given curve at a given point. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Parametric Equations |
Definition--Calculus Topics--Parametric Equations
A set of equations where each variable, x and y, is a function of a third variable, t. Graphs of parametric equations are sometimes not functions. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Hooke's Law |
Definition--Calculus Topics--Hooke's Law
A second-order differential equation that is used to model simple harmonic motion using a trigonometric function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Change of Variables |
Definition--Calculus Topics--Change of Variables
A substitution technique where a variable replaces a more complicated expression. In calculus it can simplify differentiation or integration. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Logarithmic Function |
Definition--Calculus Topics--Derivative of a Logarithmic Function
The derivative of a logarithmic function uses the laws of logarithms and the definition of e to find the derivative. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Trigonometric Function |
Definition--Calculus Topics--Trigonometric Function
One of six main functions, including sine, cosine, tangent, secant, cosecant, and cotangent. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Absolute Maximum |
Definition--Calculus Topics--Absolute Maximum
When a function takes an input value, a, for some value in the domain, such that f(a) ≥ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Vertical Asymptote |
Definition--Calculus Topics--Vertical Asymptote
A vertical line that the graph of a function approaches but does not intersect. The equation of a vertical asymptote is x = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--One-Sided Limits |
Definition--Calculus Topics--One-Sided Limits
Restricting the limit of a function for values approaching the limiting value from one side. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Integral Symbol |
Definition--Calculus Topics--Integral Symbol
The mathematical symbol used to denote the process of integration. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Average Rates of Change |
Definition--Calculus Topics--Average Rates of Change
The ratio along an interval of a domain for a given function, comparable to calculating the slope of a line. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function |
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function
Use implicit differentiation and the quotient rule to find the derivative of an inverse trig function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Inverse Function |
Definition--Calculus Topics--Inverse Function
For function f(x), the inverse function f-1(x), if it exists, undoes the mapping of the original function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Absolute Value Function |
Definition--Calculus Topics--Absolute Value Function
A piecewise function whose simplest form is shown below. These functions are not differentiable at their vertex. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Limits at Infinity |
Definition--Calculus Topics--Limits at Infinity
Finding the limiting value for function f(x) as the input value x approaches infinity. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Antiderivative |
Definition--Calculus Topics--Antiderivative
For two differentiable functions f(x) and F(x), if F'(x) = f(x), then F(x) is the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Acceleration |
Definition--Calculus Topics--Acceleration
The second derivative, with respect to time, for the displacement function. Acceleration is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Quotient Rule |
Definition--Calculus Topics--Quotient Rule
The rule for finding the derivative of a function made up of the ratios of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Integration by Substitution |
Definition--Calculus Topics--Integration by Substitution
Replacing the integrand with a simpler expression to make the process of integration easier. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Integrand |
Definition--Calculus Topics--Integrand
In the process of integration, it is the function that is being integrated. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Sum Rule |
Definition--Calculus Topics--Sum Rule
For differentiable functions f(x) and g(x) along a given interval, the derivative of the sum f(x) + g(x) is the sum of the individual derivatives f'(x) and g'(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Horizontal Asymptote |
Definition--Calculus Topics--Horizontal Asymptote
A horizontal line that the graph of a function approaches but does not intersect. The equation of a horizontal asymptote is y = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of an Exponential Function |
Definition--Calculus Topics--Derivative of an Exponential Function
The derivative of an exponential function is the product of the function and the natural log of the base. The derivative of ex is ex. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Composite Function |
Definition--Calculus Topics--Composite Function
A function whose input values are made up of another function. For two functions f(x) and g(x), a composite function can be written as f(g(x)). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Right-Hand Limit |
Definition--Calculus Topics--Right-Hand Limit
As a function f(x) approaches a specific input value a, for x-values greater than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Delta y |
Definition--Calculus Topics--Delta y
The change in y-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Displacement Function |
Definition--Calculus Topics--Displacement Function
A distance-vs.-time function used to find the distance an object has moved from a starting point. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Linear Approximation |
Definition--Calculus Topics--Linear Approximation
For differentiable function f(x), the linear approximation at x = a, for some real number a, is the equation of the line tangent to f(x) at a. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Polynomial Function |
Definition--Calculus Topics--Derivative of a Polynomial Function
The derivative of a polynomial of degree n is another polynomial of degree n - 1. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Concave Function |
Definition--Calculus Topics--Concave Function
A function whose graph curves down along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Fundamental Theorem of Calculus |
Definition--Calculus Topics--Fundamental Theorem of Calculus
The theorem that relates differentiation and integration. The two operations are basically inverses of each other. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Rolle's Theorem |
Definition--Calculus Topics--Rolle's Theorem
For function f(x) along an interval [a, b], if f(a) = f(b), then there is a point along the interval where the derivative is zero. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Oblique Asymptote |
Definition--Calculus Topics--Oblique Asymptote
A slanted line that the graph of a function approaches but does not intersect. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Second Derivative |
Definition--Calculus Topics--Second Derivative
For differentiable function f(x), the second derivative is the derivative of f'(x) and denoted as f''(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Inflection Point |
Definition--Calculus Topics--Inflection Point
The point on a curve where the curvature changes. This is often indicated by a change in the slopes of tangents to the curve. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Riemann Sum |
Definition--Calculus Topics--Riemann Sum
An approximation method for estimating the area under a curve and used to approximate the solution to a definite integral. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Composite Function |
Definition--Calculus Topics--Derivative of a Composite Function
For two functions f(x) and g(x), the derivative of the composite function f(g(x)) is f'(x)*g'(x). This is an example of the Chain Rule. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Rational Function |
Definition--Calculus Topics--Rational Function
A function made up of the ratio of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Discontinuous Function |
Definition--Calculus Topics--Discontinuous Function
A function is discontinuous if it has one or more gaps along the domain of the function. The left- or right-hand limits exist but are not equal. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Matrix Representations of Vectors |
Definition--Calculus Topics--Matrix Representations of Vectors
A vector quantity can be represented by a matrix. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Implicit Function |
Definition--Calculus Topics--Implicit Function
A function in which y cannot be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equatio |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Differential Equation |
Definition--Calculus Topics--Differential Equation
An equation that includes the derivative of a function f(x) and the variable x. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Discrete Function |
Definition--Calculus Topics--Discrete Function
A function whose graphs has gaps. This is because the function consists of separate ordered pairs or is a discontinuous function with gaps. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Local Maximum |
Definition--Calculus Topics--Local Maximum
When a function takes an input value, a, for some region in the domain, such that f(a) ≥ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Trapezoidal Rule |
Definition--Calculus Topics--Trapezoidal Rule
A technique for approximating a definite integral by adding the areas of trapezoids underneath a curve. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Convex Function |
Definition--Calculus Topics--Convex Function
A function whose graph curves up along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Continuous Functions |
Definition--Calculus Topics--Continuous Functions
A function is continuous if it has no gaps along the domain of the function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--First Derivative |
Definition--Calculus Topics--First Derivative
For differentiable function f(x), the first derivative is denoted as f'(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Linear Function |
Definition--Calculus Topics--Derivative of a Linear Function
The derivative of a linear function of the form y = mx + b is the slope of the line, m. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Asymptote |
Definition--Calculus Topics--Asymptote
A line that the graph of a function approaches but does not intersect. Asymptotes can be vertical, horizontal, or oblique. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Explicit Function |
Definition--Calculus Topics--Explicit Function
A function in which y can be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equation. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--End Behavior |
Definition--Calculus Topics--End Behavior
The way a function f(x) changes as x approaches infinity, whether positive or negative. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Limit |
Definition--Calculus Topics--Limit
As a function f(x) approaches a specific input value a, the function may approach a specific limiting value. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Separable Differential Equation |
Definition--Calculus Topics--Separable Differential Equation
A special type of differential equation in which functions f(x) and g(y) can be separated to find the solution to the equation. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Sigma Notation |
Definition--Calculus Topics--Sigma Notation
The Greek letter used for summarizing terms of a finite or infinite sequence. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Power Rule |
Definition--Calculus Topics--Power Rule
The process of finding the derivative of a power function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Delta x |
Definition--Calculus Topics--Delta x
The change in x-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Even Function |
Definition--Calculus Topics--Even Function
A function whose graph is symmetric about the y-axis. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Trig Identities |
Definition--Calculus Topics--Trig Identities
Equations that involve trigonmetric functions and are often used to simplify certain trigonometric expressions. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Extreme Value Theorem |
Definition--Calculus Topics--Extreme Value Theorem
For function f(x) along an interval, there are maximum and minimum values. If the derivative is zero along this interval, this is an inflection point. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative |
Definition--Calculus Topics--Derivative
A function used to find the slope of a tangent to a curve at a given point. The derivative is based on the following limit. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Differentiable Function |
Definition--Calculus Topics--Differentiable Function
A function is differentiable if a derivative can be found at each point in its domain. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Implicit Differentiation |
Definition--Calculus Topics--Implicit Differentiation
When a function cannot be written in the form of y as a function of x, then implicit differentation can be used to find the derivative with respect to x. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Indefinite Integral |
Definition--Calculus Topics--Indefinite Integral
The integral of a function without a specific limit on the endpoints. The result of an indefinite integral is a differentiable function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Vector |
Definition--Calculus Topics--Vector
A quantity that has magnitude and direction. Vectors are often used to model real-world phenomena such as force, speed, or acceleration. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Differentiation |
Definition--Calculus Topics--Differentiation
The process of finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Velocity |
Definition--Calculus Topics--Velocity
The first derivative, with respect to time, for the displacement function. Velocity is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Chain Rule |
Definition--Calculus Topics--Chain Rule
The process for finding the derivative of a composite function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Piecewise Function |
Definition--Calculus Topics--Piecewise Function
A function made up of separate functions, each with its own interval. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Floor Function |
Definition--Calculus Topics--Floor Function
A discrete function that takes real number values and whose output is the greatest integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Definite Integral |
Definition--Calculus Topics--Definite Integral
The integral of a function with specific limits on the endpoints. A definite integral results in a numerical value. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Rational Function |
Definition--Calculus Topics--Derivative of a Rational Function
Since a rational function is the ratio of two polynomials, the derivative of a rational function is also the ratio of two polynomials. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Ceiling Function |
Definition--Calculus Topics--Ceiling Function
A discrete function that takes real number values and whose output is the least integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Quadratic Function |
Definition--Calculus Topics--Derivative of a Quadratic Function
Since a quadratic function is a polynomial function of degree 2, the derivative is a linear function. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Integral |
Definition--Calculus Topics--Integral
A method for finding the area of a curve along an interval. In calculus, integrating a function f(x) involves finding the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--L'Hopital's Rule |
Definition--Calculus Topics--L'Hopital's Rule
For function f(x)/g(x), where f(x) and g(x) are two functions, along an interval [a, b], if there is a point c in the interval such that g(x) = 0, then L'Hopital' |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Local Minimum |
Definition--Calculus Topics--Local Minimum
When a function takes an input value, a, for some region in the domain, such that f(a) ≤ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Step Function |
Definition--Calculus Topics--Step Function
A discontinuous function whose graph looks like a staircase. A step function can be generated by ceiling or floor functions. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Zeros of a Function |
Definition--Calculus Topics--Zeros of a Function
Where the graph of a function intersects the x-axis. The solutions to the equation f(x) = 0 for some function f(x). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Absolute Minimum |
Definition--Calculus Topics--Absolute Minimum
When a function takes an input value, a, for some value in the domain, such that f(a) ≤ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Area Beneath a Curve |
Definition--Calculus Topics--Area Beneath a Curve
For a definite integral, it is the numerical result of the integration. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Odd Function |
Definition--Calculus Topics--Odd Function
A function whose graph has point symmetry about the origin. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Derivative of a Trig Function |
Definition--Calculus Topics--Derivative of a Trig Function
The derivative of a trig function is another trig function, as shown in the table. |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Intermediate Value Theorem |
Definition--Calculus Topics--Intermediate Value Theorem
For continuous function f(x) along interval [a, b] there are values between f(a) and f(b). |
Calculus Vocabulary |
| PC.F.5.5 | 
|
Definition--Calculus Topics--Power Function |
Definition--Calculus Topics--Power Function
A function with a single term that consists of a variable base raised to a real number power. The variable can also have a real number coefficient. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Math Definitions Collection--Calculus Concepts |
This collection aggregates all the definitions for key terms in a standards Calculus course. There are a total of 88 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. | Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Matrix Representations of Vectors |
Definition--Calculus Topics--Matrix Representations of Vectors
A vector quantity can be represented by a matrix. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Convex Function |
Definition--Calculus Topics--Convex Function
A function whose graph curves up along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Limits at Infinity |
Definition--Calculus Topics--Limits at Infinity
Finding the limiting value for function f(x) as the input value x approaches infinity. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Oblique Asymptote |
Definition--Calculus Topics--Oblique Asymptote
A slanted line that the graph of a function approaches but does not intersect. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Average Rates of Change |
Definition--Calculus Topics--Average Rates of Change
The ratio along an interval of a domain for a given function, comparable to calculating the slope of a line. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--L'Hopital's Rule |
Definition--Calculus Topics--L'Hopital's Rule
For function f(x)/g(x), where f(x) and g(x) are two functions, along an interval [a, b], if there is a point c in the interval such that g(x) = 0, then L'Hopital' |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Differential Equation |
Definition--Calculus Topics--Differential Equation
An equation that includes the derivative of a function f(x) and the variable x. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Inverse Function |
Definition--Calculus Topics--Inverse Function
For function f(x), the inverse function f-1(x), if it exists, undoes the mapping of the original function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative |
Definition--Calculus Topics--Derivative
A function used to find the slope of a tangent to a curve at a given point. The derivative is based on the following limit. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Concave Function |
Definition--Calculus Topics--Concave Function
A function whose graph curves down along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Instantaneous Rate of Change |
Definition--Calculus Topics--Instantaneous Rate of Change
Another way of describing the slope of the line tangent to a given curve at a given point. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--End Behavior |
Definition--Calculus Topics--End Behavior
The way a function f(x) changes as x approaches infinity, whether positive or negative. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Composite Function |
Definition--Calculus Topics--Composite Function
A function whose input values are made up of another function. For two functions f(x) and g(x), a composite function can be written as f(g(x)). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of an Exponential Function |
Definition--Calculus Topics--Derivative of an Exponential Function
The derivative of an exponential function is the product of the function and the natural log of the base. The derivative of ex is ex. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Delta x |
Definition--Calculus Topics--Delta x
The change in x-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Discontinuous Function |
Definition--Calculus Topics--Discontinuous Function
A function is discontinuous if it has one or more gaps along the domain of the function. The left- or right-hand limits exist but are not equal. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Composite Function |
Definition--Calculus Topics--Derivative of a Composite Function
For two functions f(x) and g(x), the derivative of the composite function f(g(x)) is f'(x)*g'(x). This is an example of the Chain Rule. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Power Rule |
Definition--Calculus Topics--Power Rule
The process of finding the derivative of a power function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Ceiling Function |
Definition--Calculus Topics--Ceiling Function
A discrete function that takes real number values and whose output is the least integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Parametric Equations |
Definition--Calculus Topics--Parametric Equations
A set of equations where each variable, x and y, is a function of a third variable, t. Graphs of parametric equations are sometimes not functions. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Rolle's Theorem |
Definition--Calculus Topics--Rolle's Theorem
For function f(x) along an interval [a, b], if f(a) = f(b), then there is a point along the interval where the derivative is zero. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Rational Function |
Definition--Calculus Topics--Derivative of a Rational Function
Since a rational function is the ratio of two polynomials, the derivative of a rational function is also the ratio of two polynomials. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Discrete Function |
Definition--Calculus Topics--Discrete Function
A function whose graphs has gaps. This is because the function consists of separate ordered pairs or is a discontinuous function with gaps. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Piecewise Function |
Definition--Calculus Topics--Piecewise Function
A function made up of separate functions, each with its own interval. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Integration by Substitution |
Definition--Calculus Topics--Integration by Substitution
Replacing the integrand with a simpler expression to make the process of integration easier. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Quotient Rule |
Definition--Calculus Topics--Quotient Rule
The rule for finding the derivative of a function made up of the ratios of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Extreme Value Theorem |
Definition--Calculus Topics--Extreme Value Theorem
For function f(x) along an interval, there are maximum and minimum values. If the derivative is zero along this interval, this is an inflection point. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Implicit Differentiation |
Definition--Calculus Topics--Implicit Differentiation
When a function cannot be written in the form of y as a function of x, then implicit differentation can be used to find the derivative with respect to x. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Absolute Minimum |
Definition--Calculus Topics--Absolute Minimum
When a function takes an input value, a, for some value in the domain, such that f(a) ≤ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Vertical Asymptote |
Definition--Calculus Topics--Vertical Asymptote
A vertical line that the graph of a function approaches but does not intersect. The equation of a vertical asymptote is x = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Indefinite Integral |
Definition--Calculus Topics--Indefinite Integral
The integral of a function without a specific limit on the endpoints. The result of an indefinite integral is a differentiable function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Integral |
Definition--Calculus Topics--Integral
A method for finding the area of a curve along an interval. In calculus, integrating a function f(x) involves finding the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Vector |
Definition--Calculus Topics--Vector
A quantity that has magnitude and direction. Vectors are often used to model real-world phenomena such as force, speed, or acceleration. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Hooke's Law |
Definition--Calculus Topics--Hooke's Law
A second-order differential equation that is used to model simple harmonic motion using a trigonometric function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Continuous Functions |
Definition--Calculus Topics--Continuous Functions
A function is continuous if it has no gaps along the domain of the function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Even Function |
Definition--Calculus Topics--Even Function
A function whose graph is symmetric about the y-axis. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Absolute Value Function |
Definition--Calculus Topics--Absolute Value Function
A piecewise function whose simplest form is shown below. These functions are not differentiable at their vertex. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Quadratic Function |
Definition--Calculus Topics--Derivative of a Quadratic Function
Since a quadratic function is a polynomial function of degree 2, the derivative is a linear function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Logarithmic Function |
Definition--Calculus Topics--Derivative of a Logarithmic Function
The derivative of a logarithmic function uses the laws of logarithms and the definition of e to find the derivative. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--First Derivative |
Definition--Calculus Topics--First Derivative
For differentiable function f(x), the first derivative is denoted as f'(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Integrand |
Definition--Calculus Topics--Integrand
In the process of integration, it is the function that is being integrated. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Explicit Function |
Definition--Calculus Topics--Explicit Function
A function in which y can be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equation. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Linear Function |
Definition--Calculus Topics--Derivative of a Linear Function
The derivative of a linear function of the form y = mx + b is the slope of the line, m. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Horizontal Asymptote |
Definition--Calculus Topics--Horizontal Asymptote
A horizontal line that the graph of a function approaches but does not intersect. The equation of a horizontal asymptote is y = c, for some constant c. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Sum Rule |
Definition--Calculus Topics--Sum Rule
For differentiable functions f(x) and g(x) along a given interval, the derivative of the sum f(x) + g(x) is the sum of the individual derivatives f'(x) and g'(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Zeros of a Function |
Definition--Calculus Topics--Zeros of a Function
Where the graph of a function intersects the x-axis. The solutions to the equation f(x) = 0 for some function f(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Definite Integral |
Definition--Calculus Topics--Definite Integral
The integral of a function with specific limits on the endpoints. A definite integral results in a numerical value. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Fundamental Theorem of Calculus |
Definition--Calculus Topics--Fundamental Theorem of Calculus
The theorem that relates differentiation and integration. The two operations are basically inverses of each other. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Asymptote |
Definition--Calculus Topics--Asymptote
A line that the graph of a function approaches but does not intersect. Asymptotes can be vertical, horizontal, or oblique. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Velocity |
Definition--Calculus Topics--Velocity
The first derivative, with respect to time, for the displacement function. Velocity is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Intermediate Value Theorem |
Definition--Calculus Topics--Intermediate Value Theorem
For continuous function f(x) along interval [a, b] there are values between f(a) and f(b). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Limit |
Definition--Calculus Topics--Limit
As a function f(x) approaches a specific input value a, the function may approach a specific limiting value. This limit may or may not exist. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--One-Sided Limits |
Definition--Calculus Topics--One-Sided Limits
Restricting the limit of a function for values approaching the limiting value from one side. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Rational Function |
Definition--Calculus Topics--Rational Function
A function made up of the ratio of two functions f(x) and g(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Mean Value Theorem |
Definition--Calculus Topics--Mean Value Theorem
For differentiable function f(x) along the closed interval [a, b] there is a value c within that interval such that f'(c) is parallel to the secant formed by th |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Sigma Notation |
Definition--Calculus Topics--Sigma Notation
The Greek letter used for summarizing terms of a finite or infinite sequence. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Floor Function |
Definition--Calculus Topics--Floor Function
A discrete function that takes real number values and whose output is the greatest integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Left-Hand Limit |
Definition--Calculus Topics--Left-Hand Limit
As a function f(x) approaches a specific input value a, for x-values less than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Polynomial Function |
Definition--Calculus Topics--Derivative of a Polynomial Function
The derivative of a polynomial of degree n is another polynomial of degree n - 1. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Inflection Point |
Definition--Calculus Topics--Inflection Point
The point on a curve where the curvature changes. This is often indicated by a change in the slopes of tangents to the curve. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Tangent to a Curve |
Definition--Calculus Topics--Tangent to a Curve
A line that intersects a curve at a single point and is perpendicular to the curve at that point. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Trig Identities |
Definition--Calculus Topics--Trig Identities
Equations that involve trigonmetric functions and are often used to simplify certain trigonometric expressions. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Local Maximum |
Definition--Calculus Topics--Local Maximum
When a function takes an input value, a, for some region in the domain, such that f(a) ≥ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Area Beneath a Curve |
Definition--Calculus Topics--Area Beneath a Curve
For a definite integral, it is the numerical result of the integration. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Riemann Sum |
Definition--Calculus Topics--Riemann Sum
An approximation method for estimating the area under a curve and used to approximate the solution to a definite integral. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Step Function |
Definition--Calculus Topics--Step Function
A discontinuous function whose graph looks like a staircase. A step function can be generated by ceiling or floor functions. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of a Trig Function |
Definition--Calculus Topics--Derivative of a Trig Function
The derivative of a trig function is another trig function, as shown in the table. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function |
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function
Use implicit differentiation and the quotient rule to find the derivative of an inverse trig function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Antiderivative |
Definition--Calculus Topics--Antiderivative
For two differentiable functions f(x) and F(x), if F'(x) = f(x), then F(x) is the antiderivative of f(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Separable Differential Equation |
Definition--Calculus Topics--Separable Differential Equation
A special type of differential equation in which functions f(x) and g(y) can be separated to find the solution to the equation. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Differentiation |
Definition--Calculus Topics--Differentiation
The process of finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Displacement Function |
Definition--Calculus Topics--Displacement Function
A distance-vs.-time function used to find the distance an object has moved from a starting point. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Absolute Maximum |
Definition--Calculus Topics--Absolute Maximum
When a function takes an input value, a, for some value in the domain, such that f(a) ≥ f(x), for all x in the domain. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Acceleration |
Definition--Calculus Topics--Acceleration
The second derivative, with respect to time, for the displacement function. Acceleration is a vector quantity. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Power Function |
Definition--Calculus Topics--Power Function
A function with a single term that consists of a variable base raised to a real number power. The variable can also have a real number coefficient. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Odd Function |
Definition--Calculus Topics--Odd Function
A function whose graph has point symmetry about the origin. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Trapezoidal Rule |
Definition--Calculus Topics--Trapezoidal Rule
A technique for approximating a definite integral by adding the areas of trapezoids underneath a curve. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Trigonometric Function |
Definition--Calculus Topics--Trigonometric Function
One of six main functions, including sine, cosine, tangent, secant, cosecant, and cotangent. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Linear Approximation |
Definition--Calculus Topics--Linear Approximation
For differentiable function f(x), the linear approximation at x = a, for some real number a, is the equation of the line tangent to f(x) at a. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Integral Symbol |
Definition--Calculus Topics--Integral Symbol
The mathematical symbol used to denote the process of integration. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Second Derivative |
Definition--Calculus Topics--Second Derivative
For differentiable function f(x), the second derivative is the derivative of f'(x) and denoted as f''(x). |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Implicit Function |
Definition--Calculus Topics--Implicit Function
A function in which y cannot be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equatio |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Right-Hand Limit |
Definition--Calculus Topics--Right-Hand Limit
As a function f(x) approaches a specific input value a, for x-values greater than or equal to a, the function may approach a specific limiting value. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Differentiable Function |
Definition--Calculus Topics--Differentiable Function
A function is differentiable if a derivative can be found at each point in its domain. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Delta y |
Definition--Calculus Topics--Delta y
The change in y-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Chain Rule |
Definition--Calculus Topics--Chain Rule
The process for finding the derivative of a composite function. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Change of Variables |
Definition--Calculus Topics--Change of Variables
A substitution technique where a variable replaces a more complicated expression. In calculus it can simplify differentiation or integration. |
Calculus Vocabulary |
| PC.F.5.4 | 
|
Definition--Calculus Topics--Local Minimum |
Definition--Calculus Topics--Local Minimum
When a function takes an input value, a, for some region in the domain, such that f(a) ≤ f(x), for all x in that region. |
Calculus Vocabulary |
| PC.F.5.3 | 
|
Math Video Collection: Texas Instruments Tutorial Videos |
This collection aggregates all the math videos and resources in this series: Texas Instruments Tutorial Videos. There are a total of 266 resources. | Rational Expressions, Sequences, Series, Polynomial Functions and Equations, Graphs of Quadratic Functions, Quadratic Equations and Functions, Solving Systems of Equations, Trig Expressions and Identities, Probability, Geometric Constructions with Triangles, Composite Functions, Geometric Constructions with Angles and Planes, Distance Formula, Data Analysis, Slope, Special Functions, Trigonometric Functions, Graphs of Exponential and Logarithmic Functions, Radical Functions and Equations, Rational Functions and Equations, Slope-Intercept Form, Coordinate Systems, Graphs of Linear Functions, Inequalities, Matrix Operations and Midpoint Formula |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 48 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Linear
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 49 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Quadratic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping a |
Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Trigonometric |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Trigonometric | Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Linear with Sliders |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Linear with Sliders | Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Logarithmic |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Logarithmic | Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Composite Functions, Linear to Quartic |
Closed Captioned Video: Composite Functions, Linear to Quartic | Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Polynomial |
Closed Captioned Video: Comp Functions, Lin to Polynomial
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function to a polynomial function. |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Lin w Sliders |
Closed Captioned Video: Comp Functions, Lin to Lin w Sliders
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function to another linear function using sliders. |
Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Rational |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Rational | Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Quadratic |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Quadratic | Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Cubic |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Cubic | Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 43 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Polynomial
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Rational |
Closed Captioned Video: Comp Functions, Lin to Rational
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function to a rational function. |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 39 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Cubic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore composite fun |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Composite Functions: Linear to Linear |
Closed Captioned Video: Composite Functions: Linear to Linear | Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 60 |
VIDEO: TI-Nspire Mini-Tutorial: Exploring Cosine Curve Properties Using Sliders
In this TI Nspire tutorialthe Graphing window is used to create a slider-based graph of a cosine curve to explore its properties |
Trigonometric Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Quartic |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Quartic | Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Exponential |
Closed Captioned Video: Comp Functions, Lin to Exponential
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function toan exponential function. |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 67 |
VIDEO: TI-Nspire Mini-Tutorial: Exploring Sine Curve Properties Using Sliders
In this TI Nspire tutorialthe Graphing window is used to create a slider-based graph of a sine curve to explore its properties. |
Trigonometric Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Composite Functions, Linear to Cubic |
Closed Captioned Video: Composite Functions, Linear to Cubic | Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Logarithmic |
Closed Captioned Video: Comp Functions, Lin to Logarithmic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function to a logarithmic function. |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions, Lin to Trigonometric |
Closed Captioned Video: Comp Functions, Lin to Trigonometric
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one linear function to a trigonometric function. |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 45 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Radical
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 47 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Trigonometric
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mappi |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 46 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Rational
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping on |
Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Linear |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions: Linear to Linear
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Composite Functions: Linear to Linear. |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Composite Functions, Linear to Radical |
Closed Captioned Video: Composite Functions, Linear to Radical | Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 41 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Linear with Sliders
In this TI Nspire tutorial for the TI-Nspire CAS, we explore |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 40 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Exponential
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping |
Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Polynomial |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Polynomial | Composite Functions |
| PC.F.5.3 | 
|
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Radical |
Video Transcript: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Radical | Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 69 |
VIDEO: TI-Nspire Mini-Tutorial: Finding the Intersection Point of Two Graphs
In this TI Nspire tutorial, the Graph window is used to graph two functions and finding the point of intersection. |
Coordinate Systems |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 42 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Logarithmic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping |
Composite Functions |
| PC.F.5.3 | 
|
Closed Captioned Video: Comp Functions: Lin to Quadratic |
Closed Captioned Video: Comp Functions: Lin to Quadratic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping a linear function to a quadratic. |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 44 |
VIDEO: TI-Nspire Mini-Tutorial: Composite Functions, Linear to Quartic
In this TI Nspire tutorial for the TI-Nspire CAS, we explore mapping one |
Composite Functions |
| PC.F.5.3 | 
|
VIDEO: Ti-Nspire Mini-Tutorial, Video 59 |
VIDEO: TI-Nspire Mini-Tutorial: Exploring Composite Functions | Composite Functions |
| PC.F.5.1 | 
|
Math Definitions Collection--Calculus Concepts |
This collection aggregates all the definitions for key terms in a standards Calculus course. There are a total of 88 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. | Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Integrand |
Definition--Calculus Topics--Integrand
In the process of integration, it is the function that is being integrated. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Discontinuous Function |
Definition--Calculus Topics--Discontinuous Function
A function is discontinuous if it has one or more gaps along the domain of the function. The left- or right-hand limits exist but are not equal. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Change of Variables |
Definition--Calculus Topics--Change of Variables
A substitution technique where a variable replaces a more complicated expression. In calculus it can simplify differentiation or integration. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Chain Rule |
Definition--Calculus Topics--Chain Rule
The process for finding the derivative of a composite function. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Differentiation |
Definition--Calculus Topics--Differentiation
The process of finding the derivative of a function. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--End Behavior |
Definition--Calculus Topics--End Behavior
The way a function f(x) changes as x approaches infinity, whether positive or negative. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Displacement Function |
Definition--Calculus Topics--Displacement Function
A distance-vs.-time function used to find the distance an object has moved from a starting point. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Ceiling Function |
Definition--Calculus Topics--Ceiling Function
A discrete function that takes real number values and whose output is the least integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Discrete Function |
Definition--Calculus Topics--Discrete Function
A function whose graphs has gaps. This is because the function consists of separate ordered pairs or is a discontinuous function with gaps. |
Calculus Vocabulary |
| PC.F.5.1 | 
|
Definition--Calculus Topics--Composite Function |
Definition--Calculus Topics--Composite Function
A function whose input values are made up of another function. For two functions f(x) and g(x), a composite function can be written as f(g(x)). |
Calculus Vocabulary |
