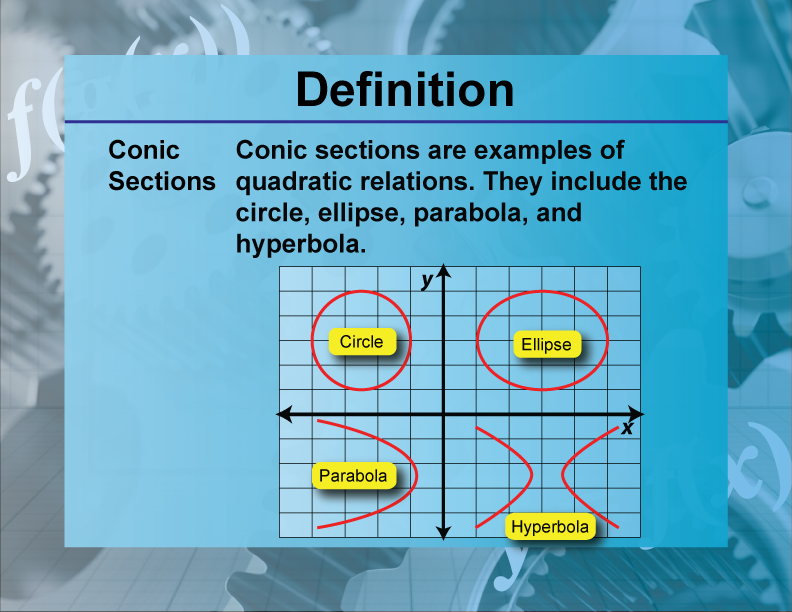
Definition--Functions and Relations Concepts--Conic Sections
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Functions and Relations >> Conic Sections

Definition--Functions and Relations Concepts--Conic Sections

Conic Sections

Conic Sections Image

Topic

Functions and Relations

Definition

Conic sections are the curves obtained by intersecting a plane with a double-napped cone.

Description

Conic sections include circles, ellipses, parabolas, and hyperbolas, which are fundamental in the study of geometry and algebra. These shapes are described by quadratic equations and have numerous applications in physics, engineering, and astronomy. For example, the orbits of planets are ellipses, and parabolic mirrors are used in telescopes and satellite dishes. The general quadratic equation for conic sections is 

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0

Understanding conic sections is crucial for solving geometric problems and for applications in designing optical systems and analyzing planetary motion.

For a complete collection of terms related to functions and relations click on this link: Functions and Relations Collection

Common Core Standards CCSS.MATH.CONTENT.8.F.A.1, CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.B.3, CCSS.MATH.CONTENT.HSF.BF.B.4
Grade Range 6 - 9
Curriculum Nodes Algebra
    • Functions and Relations
        • Conic Sections
Copyright Year 2013
Keywords definition, function, relations, glossary terms