Display Title
Definition--Calculus Topics--Horizontal Asymptote
Display Title
Definition--Calculus Topics--Horizontal Asymptote
Definition--Calculus Topics--Horizontal Asymptote
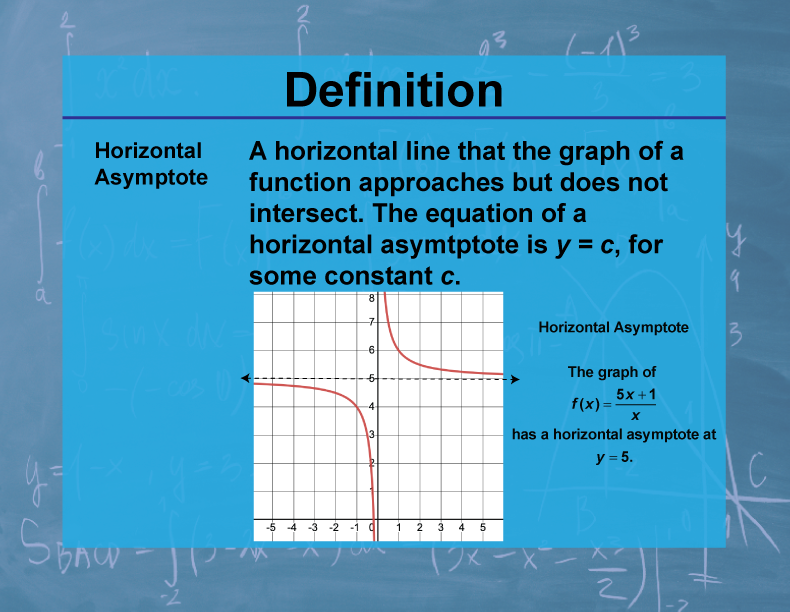
A horizontal line that the graph of a function approaches but does not intersect. The equation of a horizontal asymptote is y = c, for some constant c.
— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —
To see the complete collection of Calculus terms, click on this link.
| Grade Range | 11 - 12 |
|---|---|
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |