Display Title
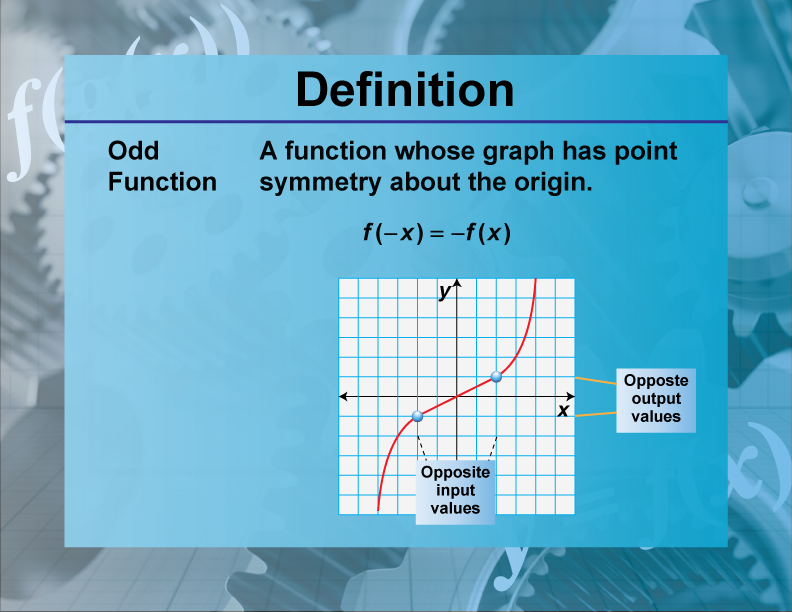
Definition--Functions and Relations Concepts--Odd Function
Display Title
Definition--Functions and Relations Concepts--Odd Function
Definition--Functions and Relations Concepts--Odd Function
This is a collection of definitions related to the topic of functions and relations. This includes general definitions for functions and relations, as well as terms related to types of functions, visualization models, other related terms.
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math definitions on this topic. To see the complete collection of definitions, click on this Link.
To learn more about Slide Show Creator, click on this Link.
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.1, CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.B.3, CCSS.MATH.CONTENT.HSF.BF.B.4 |
|---|---|
| Grade Range | 6 - 9 |
| Curriculum Nodes |
Algebra • Functions and Relations • Relations and Functions |
| Copyright Year | 2021 |
| Keywords | definition, function, relations, glossary terms |