
Display Title
Video Tutorial: Ratios, Video 2
Display Title
Video Tutorial: Ratios: Ratios with Three Items
This is part of a collection of video tutorials on the topic of Ratios and Proportions. This series includes a complete overview of ratios, equivalent ratios, rates, unit rates, and proportions. The following section will provide additional background information for the complete series of videos.
What Are Ratios?
A ratio is the relationship between two or more quantities among a group of items. The purpose of a ratio is find the relationship between two or more items in the collection.
Let's look at an example.
Here is a collection of coins. There are four pennies and two dimes, for a total of six coins. The ratio of pennies to dimes can be expressed as a ratio, and a ratio can be written in three different, but equivalent ways. One of the ways to express ratios is as a fraction. Do you see it?
When expressed as fractions, ratios can then be rewritten as fractions in simplest form. Notice that the ratio of pennies to dimes is 4 to 2, which, as a fraction, can be written as 2 to 1.
For some groupings, you can write a ratio that includes three terms.
Ratios usually include similar types of objects. Here is a collection of different types of balls.
What Are Rates?
Rates are a special type of ratio. Rates involve different types of quantities. Here is an example of a rate involving cost and weight.
How Are Fractions Different From Ratios?
Although ratios can look fractions, they are different from fractions. Here is a collection of coins.

The ratio of dimes to quarters is 2:3, which can be expressed as a fraction, 2/3. Does that mean that two thirds of the coins are dimes? No, in fact, the fraction dimes is 2/12, or 1/6.
Why are there to different fractions? The ratio of dimes to quarters is a part-to-part ratio. The fraction of dimes is the a part-whole relationship.
Ratios, when expressed as fractions, are part-to-part ratios. This is why the ratio of quarters to pennies is 1:1, while the fraction of quarters is 1/3.
Do you see the difference between ratios and fractions?
What Are Equivalent Ratios?
Ratios express a part-to-part relationship between two items in a group of items. Equivalent ratios result when the ratios expressed as fractions are equal. Let's look at an example.

This is a collection of colored circles. First, look at the ratio of green : yellow.
2 : 4
Now look at the ratio of orange : red.
1 : 2
But when written as fractions 1/2 and 2/4 are equivalent fractions. This also means they are equivalent ratios.
What Are Proportions?
When two ratios are equivalent, they form a proportion. In the previous section you saw that the ratio green : yellow was equivalent to orange : red. Because they are equivalent ratios, they form a proportion.
When two quantities are proportional, then corresponding parts are proportional. Let's look at an example.
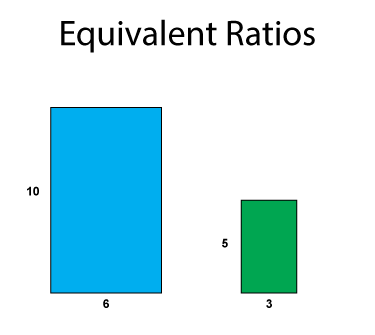
These two rectangles are proportional. That means that the ratio of length : width for the rectangles form equivalent ratios.
For the blue rectangle the ratio is 10 : 6. For the green rectangle the ratio is 5 : 3. Do you see that these are equivalent ratios?
When measurement ratios like this are equivalent, then the rectangles are proportional. Another way of saying this is that the rectangles are similar. When two geometric figures are similar, that means they have the same shape, but not necessarily the same size.
Solving Proportions
When two measurements are proportional--or you want them to be proportional--then you can solve a proportion. Solving a proportion is the same as solving an equation. Let's look at an example.
Here are two similar rectangles.

The blue rectangle has sides of 10 by 4. The red rectangle has sides of 10 by x. Since the figures are similar, or proportional, then we can solve the following equation.
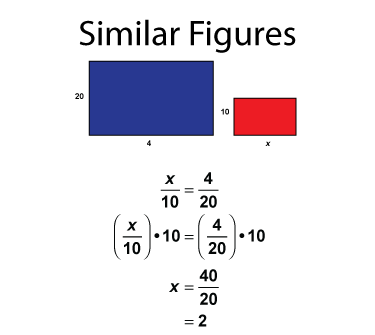
The first line of the equation are the two equivalent ratios. The unknown, x, is the side length of the blue rectangle. Solving for x shows the measurement that ensures the rectangles are similar.
When solving a proportion, there are four quantities, one of which is unknown, usually represented by the variable x. Solving the proportion usually means solving for x. In the example above, with geometric figures, solving the proportion is also called creating a scale drawing.
Creating scale models is an example of solving proportions. When you see a scale model with a given ratio (for example, a 1:10 scale model) that means that the model is proportional to the original, scaled down by the ratio down. This is an example where a ratio does represent a fractional amount.
To see the complete collection of the video tutorials on this topic, click on this link.
Note: The download is an MP4 video file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Video Library
To see the complete collection of math videos, click on this link.
Closed Captioned Video Library
This video is available in closed captioned format. To see the complete collection of captioned videos, click on this link.
Video Transcripts
This video has a transcript available. To see the complete collection of video transcripts, click on this link.
| Common Core Standards | CCSS.MATH.CONTENT.6.RP.A.2, CCSS.MATH.CONTENT.6.RP.A.1, CCSS.MATH.CONTENT.7.RP.A.1 |
|---|---|
| Duration | 4.50 minutes |
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Ratios, Proportions, and Percents • Ratios and Rates |
| Copyright Year | 2016 |
| Keywords | ratios, ratios with more than one term, video tutorial |