
Display Title
Video Tutorial: Fractions, Video 18
Display Title
Video Tutorial: Fractions: Dividing Two Fractions
This is part of a collection of video tutorials on the topic of Fractions. This includes defining fractions, fraction operations, equivalent fractions, comparing and ordering fractions, and applications of fractions.
—PRESS PREVIEW TO SEE THE VIDEO TUTORIAL—
To see the complete collection of these videos on fractions, click on this link.
The following section includes background information on fractions. Refer to this section as you view the videos, or as review material afterward.
What Are Fractions?
Fractions are numbers. Even though they represents parts of a larger whole, they are still numbers, just like any other number.
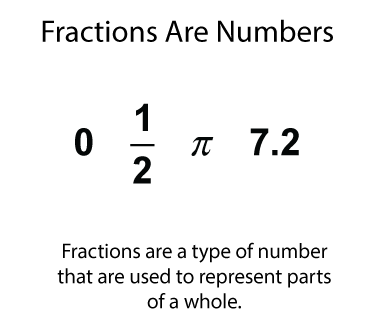
You're accustomed to counting by whole numbers, but you can also count by fractional amounts. In fact, you have been probably been counting by fractions without even realizing it. Here are just two examples.

A fraction has two main parts, the numerator and the denominator. Each is a whole number (or an integer) and the denominator cannot be zero.

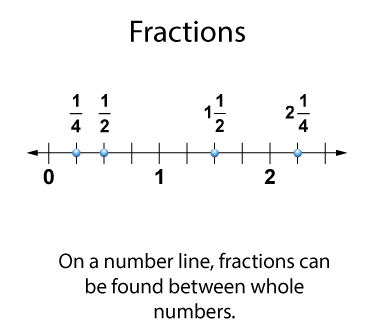
On a number line, fractions are found between whole number values. Take a look at this number line and you'll see some fractional values.
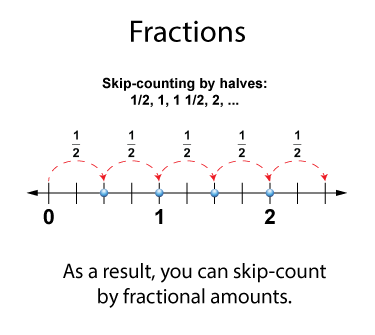
From your experience with whole numbers, you know that you can skip-count by numbers greater than 1. You can also skip-count by fractions. Take a look at this example, which shows how to skip-count by 1/2.
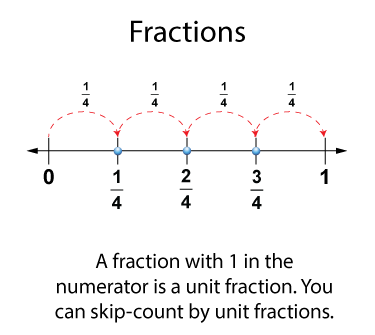
From your work with skip-counting, each count increases by the same amount. When skip-counting by fractions, each fractional step is the same value. For now let's focus on fractions between 0 and 1, specifically fourths.

You can see how each of the fourths is equally spaced from 0 to 1. Notice that each fraction has the same denominator. Also, the numerators increase in value by 1.

Notice the first fraction, 1/4. When a fraction has a 1 in the numerator, it is called a unit fraction. You can skip-count by this unit fraction from 0 to 1.
Counting by a unit fraction shows that all the fractions that share that denominator are equally spaced from 0 to 1. Do you see that?
Here is the same idea, now shown with 1/3.
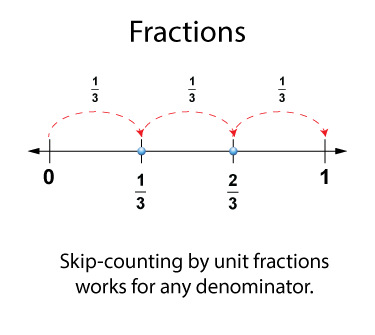
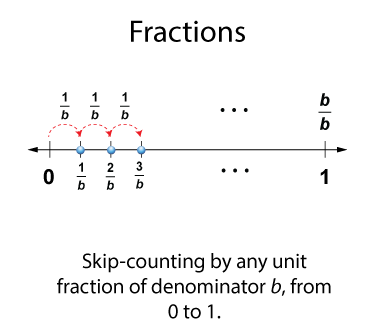
We generalize this idea to any unit fraction 1/b.
Area Models for Fractions
Another way to represent fractions involves an area models. Here are two examples of such models.
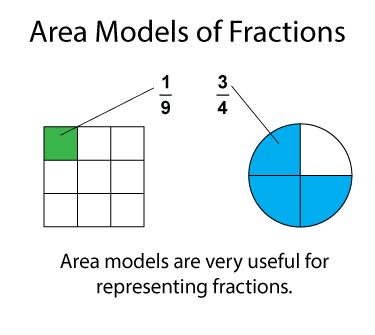
Area models for fractions have certain properties. The area is broken up into smaller sections of equal size. If the sections are not the same size, then it cannot be used to model fractions.

When the area model has equal-sized sections, then the total number of those sections represents the denominator of any fractions it models. With an area model, the shaded region represents the numerator of the fraction. See below.

Fraction models can also be used to represent real things. Pizzas sliced into equal slices are a good representation of fractions. See below.

Equivalent Fractions
When two fractions represent the same amount of area, then the fractions are called equivalent fractions. Here are two pizzas sliced into fourths and eighths. Each set of slices represent the same area but two different fractions. However, since they have the same area, then the fractions are equivalent.
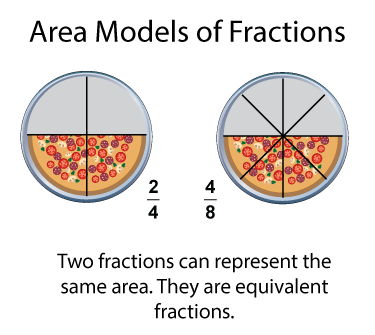
Equivalent fractions have the same location on a number line. From the previous example you saw that 2/4 and 4/8 are equivalent fractions. Below you can see that those same fractions have identical locations on a number line.

There are several ways of generating equivalent fractions. For area models make sure the two fractions have the same area and make sure the sub sections are of equal size. Here is an example.
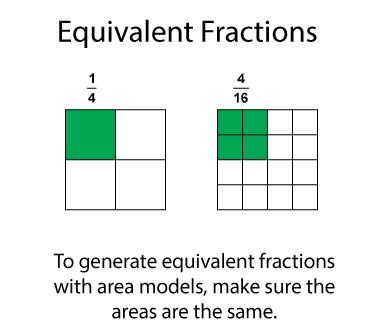
You can generate equivalent fractions numerically by multiplying the numerator and denominator by the same number. Here are fractions equivalent to 1/2.

Any fraction can generate equivalent fractions. In fact, an infinite number of equivalent fractions can be generated.
Simplifying Fractions
Working backward from the process of generating equivalent fractions, you can use the idea to simplify a fraction. Here's how it works. We start with the fraction 4/20. You can rewrite with a common factor of 4 on both the numerator and denominator, which divides out, leaving the fraction in simplest form, 1/5.

A fraction in simplest form has no more common factors (other than 1) in both the numerator and denominator.
Common Denominators
When two fractions have the same denominator, we describe that as having a common denominator. For example, 1/4 and 3/4 have a common denominator of 4.
Finding the common denominator for two fractions is very useful if you're comparing the fractions or adding and subtracting them. Using the technique of generating equivalent fractions is very useful for finding a common denominator. Here is an example.

So, if you were comparing or adding 1/5 and 1/3, finding the common denominator makes either task much easier.
To see the complete collection of the video tutorials on this topic, click on this link.
Note: The download is an MP4 video file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Video Library
To see the complete collection of math videos, click on this link.
Closed Captioned Video Library
This video is available in closed captioned format. To see the complete collection of captioned videos, click on this link.
Video Transcripts
This video has a transcript available. To see the complete collection of video transcripts, click on this link.
| Common Core Standards | CCSS.MATH.CONTENT.5.NF.B.5, CCSS.MATH.CONTENT.4.NF.A.1 |
|---|---|
| Duration | 4.00 minutes |
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Arithmetic • Fractions • Fractions and Mixed Numbers |
| Copyright Year | 2017 |
| Keywords | fractions, dividing fractions, video tutorial, video tutorials, fractions video tutorials, video tutorial |