
Display Title
Video Tutorial: Algebra Tiles 3
Display Title
Video Tutorial: Algebra Tiles: Modeling Negative Integers Using Algebra Tiles
Description
This is part of a collection of video tutorials the topic of Algebra Tiles.This series of videos describes what algebra tiles are and how they can be used to model numbers, operations, expressions, and equations. Use this series if you are incorporating the use of algebra tiles in your instruction.
—CLICK PREVIEW TO SEE THE VIDEO TUTORIAL—
To see the complete collection of the video tutorials on this topic, click on this link.
The following section reviews the basics of algebra tiles. Use this material as background material, and also as a supplement to the video series.
What Are Algebra Tiles?
Algebra Tiles are a very useful numerical model for positive integers, negative integers, and even variables. Algebra tiles usually come in three main colors: red, yellow, and green.
- The red tiles model negative numbers.
- The yellow tiles model positive numbers.
- Green tiles model unknown quantities, such as the variable x.
Each tile represents a quantity. For example, one red tile represents -1 and two yellow tiles represent +2.
Modeling Integers Using Algebra Tiles
The set of integers includes zero, positive whole numbers, and negative whole numbers. Integers are represented by this set:
{...-3, -2, -1, 0, 1, 2, 3...}
Algebra tiles are very useful for modeling integers. This is especially useful when first introducing the idea of negative numbers. The red and yellow tiles clearly demonstrate that these are different types of numbers.
Here are examples of modeling positive integers using algebra tiles. The number of tiles represents the numerical value of the integer.
Here are examples of modeling negative integers using algebra tiles. Once again, make a note of the number of tiles and the number that they represent.
Modeling Zero
You can even model zero by placing a positive tile and a negative tile next to each other. This is called a zero pair. By placing one yellow tile next to one red tile, they form a zero pair because of the following fact:
1 + (-1) = 0
There are even multiple ways of modeling zero, so long as equal numbers of red and yellow tiles are used.
Why is it necessary to model zero using algebra tiles? As you'll see, when it comes to solving equations using algebra tiles, creating zero pairs is an important part of the process.
Adding Integers Using Algebra Tiles
When you're working with number models, you can also model basic operations. Here we look at adding and subtracting integers using algebra tiles.
If you're adding two positive integers, you can use algebra tiles to model the sum. Here's an example. Notice that the sum is positive.
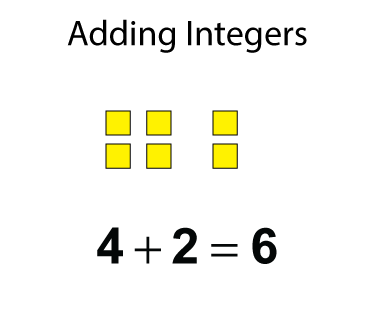
The same idea applies to adding two negative integers. Take a look at this example. Notice that the sum is negative.

When you're adding integers that are a mix of positive and negative numbers, use an algebra tiles model to form zero pairs to find the sum. Here is an example.
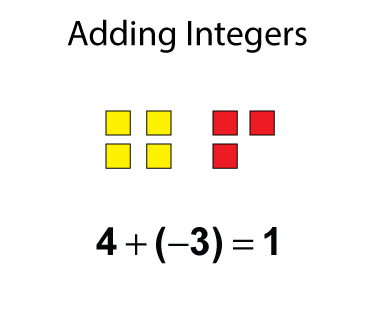
Subtracting Integers Using Algebra Tiles
Modeling subtraction with algebra tiles involves the familiar "take away" model. Here's a simple example. Start with the algebra tiles and then take away the number needed. What's left is the difference.
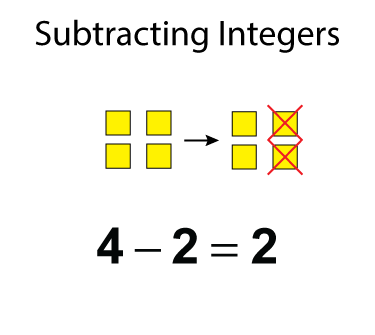
In this example, we have four positive tiles and want to take two away. Since there are four tiles there, then taking two away leaves two tiles.
But what if there are no tiles to "take away"? For example, how would you use algebra tiles to model this subtraction expression?
4 – (-2)
If there are four positive tiles (yellow), how can we take away two negative tiles (red)? This is where you use zero pairs. Look at this example.
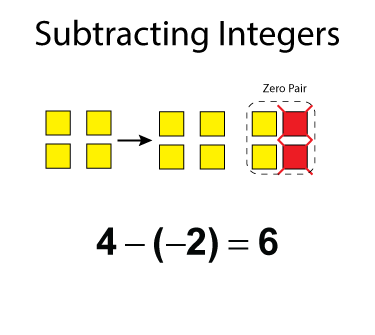
We start with four yellow tiles (+4), but we can't take away any red tiles. So, add a zero pair that includes two red tiles. Notice the zero pair on the right. Now take away the red tiles and what's left over (+6) is the difference.
Modeling Expressions
An algebraic expression includes a variable and a number. Here is an example of an algebraic expression:
x + 4
Algebra tiles can also be used to model algebraic expressions. To model such expressions, use the tall green tile to model the variable. Take a look at these examples. Make a note of the type of algebra tile used and its color.
Modeling Equations
When an algebraic expression equals a number, then an equation is formed. Here's such an equation.
x + 2 = 1
You can also use algebra tiles to model and solve equations.
This is where zero pairs come into play when solving equations. Use zero pairs to solve for the variable. In the equation shown above, add two red tiles to both sides of the equation to cancel out the two yellow tiles on the left. The result is shown below.
Note: The download is an MP4 video file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Video Library
To see the complete collection of math videos, click on this link.
Closed Captioned Video Library
This video is available in closed captioned format. To see the complete collection of captioned videos, click on this link.
Video Transcripts
This video has a transcript available. To see the complete collection of video transcripts, click on this link.
| Common Core Standards | CCSS.MATH.CONTENT.6.NS.C.6.A, CCSS.MATH.CONTENT.6.EE.B.5, CCSS.MATH.CONTENT.7.EE.B.3, CCSS.MATH.CONTENT.6.NS.C.6.C, CCSS.MATH.CONTENT.7.NS.A.1.A, CCSS.MATH.CONTENT.7.NS.A.1.B, CCSS.MATH.CONTENT.7.NS.A.2.B |
|---|---|
| Duration | 2.67 minutes |
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Algebra Tiles--Expressions and Equations |
| Copyright Year | 2016 |
| Keywords | algebra tiles, negative integers, video tutorial |