
Display Title
Definition--Rationals and Radicals--Rational Equations
Display Title
Definition--Rationals and Radicals--Rational Equations
This is part of a collection of definitions related to the concepts of rational and radical expressions, functions, and equations. These downloadable images can easily be incorporated into your lesson plans.
—CLICK PREVIEW TO SEE THE DEFINITION CARD—
To see the complete collection of definitions on this topic, click on this link.
The next section provide a review of rational numbers, expression, functions, and equations. This includes a video, with transcript. It's important to understand the basics of rational numbers in order to fully understand rational expressions, functions, and equations. This review section provides a complete background on rationals.
What Are Rational Numbers?

The video was uploaded on 10/22/2022.
You can view the video here.
The video lasts for 6 minutes and 17 seconds.
Video Transcript
In your study of integers you saw that dividing integers sometimes resulted in a non-integer quotient.
In this video we look at a class of numbers called rational numbers, which also includes the integers.
Let’s start with an example.
Use the illustration to determine the ratio of boys to girls in the class, the fraction of boys in the class, and the fraction of girls in the class. Display the results as rational numbers.
A rational number is the ratio of two integers a and b, where b is not zero. The simple reason that b can’t be zero is that division by zero is undefined. As written, a rational number looks like a fraction or a ratio, but integers can also be rational numbers. We’ll see examples of those later in the video.
In this example, we are given a classroom of boys and girls.
The first task is to find the ratio of boys to girls.
Count the number of boys.
As you can see there are 1-2-3-4-5-6-7 boys.
Now count the number of girls. There are 1-2-3-4-5-6-7-8-9 girls. So the ratio of boys to girls is shown here.
The ratio is 7/9 or 7 to 9.
This is a rational number, since it meets the definition of a ratio of two integers, here and here. Now we need to calculate the fraction of boys in the classroom. This is a different ratio.
We know the number of boys is 7, now we need to find the total number of students. We can add these two numbers, 7 + 9, to get 16.
Or we could see that the array here is 2 by 8, which also gives us 16. So the fraction of boys is 7/16.
This is also a rational number.
Finally, the fraction of girls is 9/16, also a rational number.
There are a couple more observations to make.
First, the total number of students, the whole, is made up of two parts, the number of boys and the number of girls.
So the ratio of boys to girls, this ratio, is a part to part ratio.
The fraction of boys and girls are part-whole ratios.
All of these are rational numbers, but some are fractional amounts. Let’s look at another example.
On the number line, each tic mark represents a quarter inch. Describe the positions of the fish and the dragonfly using rational numbers. With this vertical number line, the water line is the zero mark, as shown here. We are told that each tic mark represents a quarter. Let’s start with the dragonfly and find its position. Starting at zero there are 1-2-3-4-5 tic marks, so the dragonfly is at position 5/4, as shown here.
This is also equivalent to 1 ¼.
Now let’s find the position of the fish. Starting at zero, there are 1-2 tic marks. Since this position is below the zero mark, the number is negative. So the fish is at position -2/4, which is also equal to -½. We rewrite the positions on the number line as a mixed number here and a fraction in simplest form here. These are rational numbers because they meet the definition of a rational number. Even the mixed number can be rewritten as an improper fraction. Let’s look at a final example.
On a winter day in a given city the low and high temperatures for the day are shown in this double bar graph. Describe these temperatures relative to 0°F. Are these temperatures rational numbers?
Another way to express rational numbers are as decimals.
The data shown in this graph shows values to the tenths place. However, not all values written in decimal form are rational numbers. For example, π is not a rational number.
The horizontal line represents 0°F.
So, this bar represents a temperature of 25.8° above zero, and this temperature represents -10.5 degrees below zero. How do we know that these decimals are rational numbers? Going back to the definition of a rational number, 25.8 can be rewritten as 258 over 10, which in simplest form is 129 over 5.
Likewise, -10.5 can be rewritten as -105 over 10, which simplifies to -21 over 2. When a decimal can be written as a ratio of two integers, with a non-zero term in the denominator, then the decimal is a rational number.
Defining Rational Numbers
All rational numbers can be written as shown below. A rational number looks like a fraction, but it is a ratio of two numbers. As with fractions, the denominator cannot be zero.
Rational numbers can be written in different ways.
Integers are examples of rational numbers.
If a number cannot be written as the ratio of two integers, then it is an irrational number.
Rational numbers can be graphed on a number line. Make a note of the rational numbers in decimal form graphed on the number line below. However, keep in mind that the integer values are also rational numbers.
Rational numbers and their opposites, as with integers, add up to zero. Every rational number has its opposite.
Adding and Subtracting Rational Numbers
Add and subtract rational numbers the way you would add fractions. Here is an example of combining a positive and negative rational number.
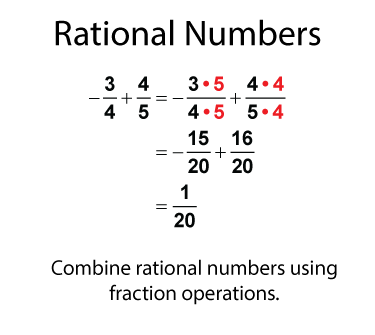
Here is another example. In this example the result is a negative number.
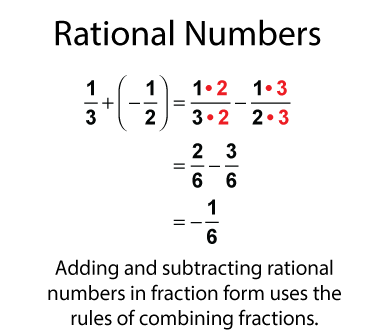
Adding and subtracting rational numbers in fraction form is a lot like adding and subtraction fractions. The main difference is that these fractions can be negative.
When expressed as decimals, combine rational numbers the way you would decimals.
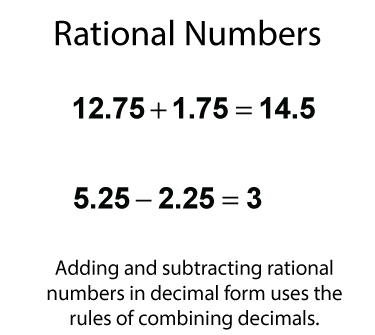
Adding and subtracting rational numbers in decimal form is a lot like adding and subtraction decimals. The main difference is that these decimals can be negative.
Multiplying Rational Numbers
Multiply rational numbers the way you would multiply fractions. Here are examples of multiplying rational numbers. The second example shows how to divide out common factors before multiplying.
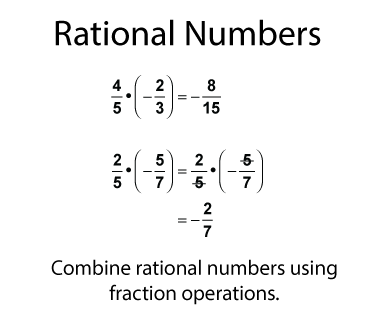
Multiplying rational numbers in fraction form is a lot like multiplying fractions. The main difference is that these fractions can be negative.
Rational Expressions
Rational numbers are ratios of two integers. Similarly, a rational expression is the ratio of two algebraic expressions. The algebraic expression can be a number or a polynomial. Here are three examples of rational expressions.
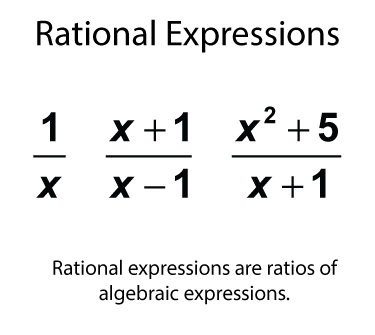
Like rational numbers, the denominator can't be zero. Let's see what that looks like for the expressions above.
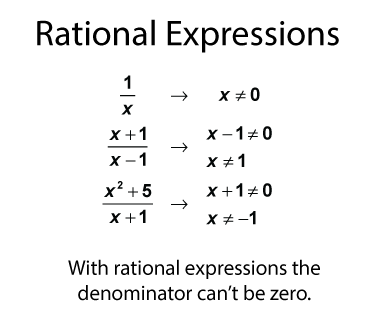
Like rational numbers, rational expressions can be combined. Use fraction operations to combine rational expressions.
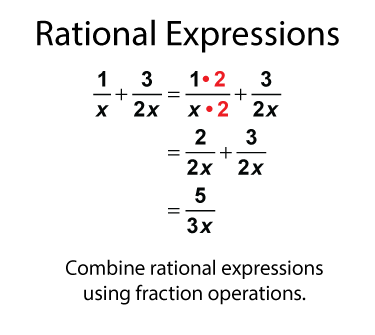
Simplify rational expressions by finding common factors in the numerator and denominator. In this example there is a common term, x + 1, that divides out of both the numerator and denominator.
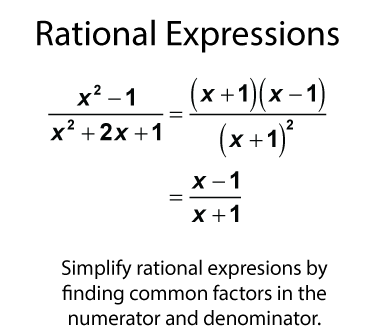
Rational Equations
When a rational expression equals a number, this forms a rational equation, which can be solved for the variable. Here is an example of a rational equation and its solution.
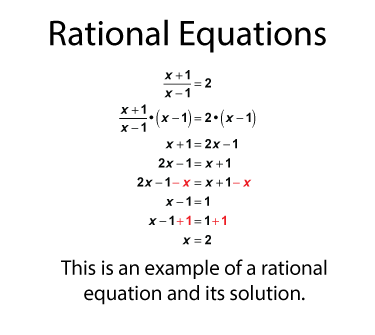
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math definitions on this topic. To see the complete collection of definitions, click on this link.
To learn more about Slide Show Creator, click on this Link.
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.HSA.REI.A.2, CCSS.MATH.CONTENT.HSN.RN.A.1, CCSS.MATH.CONTENT.HSF.IF.C.7 |
|---|---|
| Grade Range | 8 - 12 |
| Curriculum Nodes |
Algebra • Rational Expressions and Functions • Rational Functions and Equations |
| Copyright Year | 2022 |
| Keywords | radicals, radical expressions, rational numbers, rational expressions, definitions, glossary term, rational functions |