Display Title
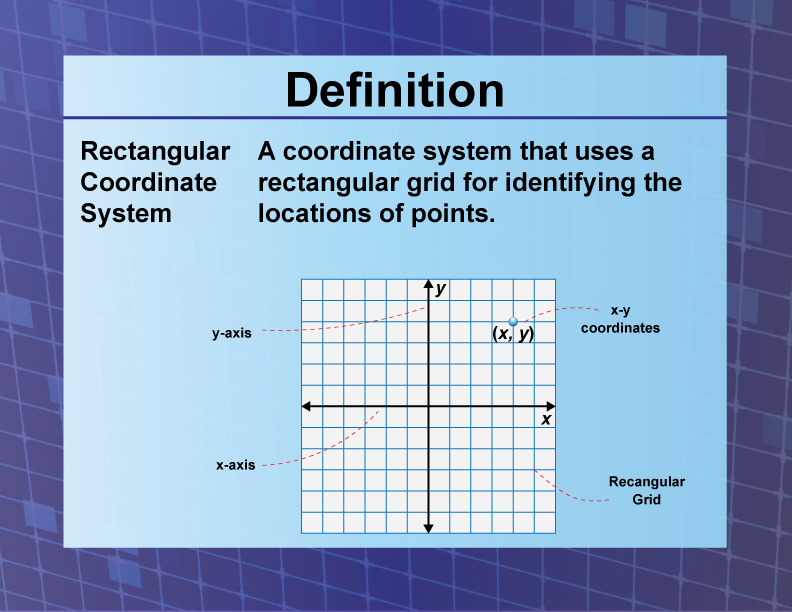
Definition--Coordinate Systems--Rectangular Coordinate System
Display Title
Definition | Coordinate Systems | Rectangular Coordinate System
This is part of a collection of definitions related to coordinate systems and related topics. This includes general definitions for coordinate systems, as well as examples of specific coordinate systems and properties of those systems.
—PRESS PREVIEW TO SEE THE DEFINITION—
To see the complete collection of definitions, click on this link.
The following section includes background information on the Cartesian coordinate plane.
Integers on the Cartesian Coordinate Plane

The video was uploaded on 11/15/2022.
You can view the video here.
The video lasts for 6 minutes and 44 seconds.
Video Transcript
You’ve seen how to add, subtract, multiply, and divide integers. You have also seen how to simplify expressions with integers. In this video we look at using integers to graph points on the Cartesian coordinate plane.
Let’s start with an example.
A construction truck goes from Building A to Building B to Building C. Describe the coordinates of these buildings.
Notice the Cartesian coordinate system. Here is the y-axis and here is the x-axis. This happens to just show Quadrant I.
This truck goes from point A here to point B here to point C here. These three points can be graphed with integer coordinates.
Here is a version of the graph with just the points. Where the x- and y-axes intersect is the origin, which has coordinates (0, 0).
Let’s assume that each tic mark along the horizontal and vertical axes represent 1 unit. Let’s look at point A. We start at the origin and count one unit along the x-axis until we are aligned with A. Now we move up 2 units to get to the point. So, point A has coordinates (1, 2).
This number is the x-coordinate and this number is the y-coordinate. Now let’s look at point B.
Start at the origin and count the number of tic marks along the x-axis to align with B. There are 1-2-3-4-5-6-7-8 units. And we move up 2 units. So point B has coordinates (8, 2).
Now let’s move on to point C. First thing, notice that it is vertically aligned with point B, which we know has an x-coordinate of 8. So C has an x-coordinate of 8. Starting here let’s count up to get to C. There are 1-2-3-4-5 tic marks. So C has coordinates (8, 5).
Let’s look at another example.
A diver takes a dive and his path is shown in the red dotted line. He passes through points A, B, and C. What are the coordinates of those points?
We can use positive and negative integers to show the coordinates of the diver at the three points. Here is a clean version to make it easier to identify the coordinates.
Recall that where the x- and y axes intersect is the origin, which has coordinates (0, 0). This coordinate system shows Quadrant I here and Quadrant II here. Quadrant I has all positive coordinates. Quadrant II has positive x and negative y coordinates.
Let’s assume that each tic mark along the horizontal and vertical axes represent 1 unit. Let’s look at point A. We start at the origin and count one unit along the x-axis until we are aligned with A. There are 1-2-3-4-5-6-7-8-9-10 units. Now we move up 1-2-3-4 units to get to the point. So, point A has coordinates (10, 4).
Now let’s look at point B. Notice that the point is on the x-axis. Any point on the x-axis has zero as a y-coordinate. So we just need t find the x-coordinate.
Start at the origin and count one unit along the x-axis until we are aligned with B, There are 1-2-3-4-5-6-7-8-9-10-11-12-13-14-15 units. So point B has coordinates (15, 0).
Now let’s move on to point C. First thing, notice that it is just one unit to the right of point B. Since point B has an x-coordinate of 15, then C has an x-coordinate of 16. Now we count down 1-2-3-4 units along the y-axis. Four units below the x-axis makes the x-coordinate -4. So point C has coordinates (16, -4).
Let’s look at a final example.
Find the coordinates of points A, B, C, and D, which are the corners of a rectangle.
Notice that this rectangle is centered at the origin. What this means is that the y-axis splits the rectangle into equal sections. The same thing happens with the x-axis: It splits the rectangle into two equal sections this way.
This means that the rectangle is symmetric about the x-axis and the y-axis. Now we can look at the coordinates for the four points to see how this symmetry is reflected in the coordinates.
Notice that positive and negative 7 and 3 are integers that make up these coordinates. Look at any collinear pair of coordinates and you’ll see that pairs of coordinates are opposites. For example, A and B have opposite x-coordinates, while D and C also have opposite x-coordinates. A-D and BC have opposite y-coordinates.
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math definitions on this topic. To see the complete collection of definitions, click on this Link.
To learn more about Slide Show Creator, click on this Link.
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.6.G.A.3, CCSS.MATH.CONTENT.5.G.A.1, CCSS.MATH.CONTENT.5.G.A.2, CCSS.MATH.CONTENT.6.NS.C.6.C, CCSS.MATH.CONTENT.8.G.A.3 |
|---|---|
| Grade Range | 5 - 8 |
| Curriculum Nodes |
Geometry • Coordinate Geometry • Coordinate Systems |
| Copyright Year | 2021 |
| Keywords | defnitions, glossary terms, coordinate geometry, ordered pair, coordinates, quadrant |