Circle

Topic

Circles

Definition

A circle is a set of all points in a plane equidistant from a given point, the center.

Description

The circle is one of the most fundamental shapes in geometry, characterized by its symmetry and uniformity. It is used extensively in various fields, including engineering, design, and astronomy, where its properties are applied to create wheels, gears, and orbits. Mathematically, a circle is defined by its center and radius, and its equation in a plane is 

(x − h)² + (y − k)² = r² 

Understanding circles is crucial in math education as it provides a basis for exploring more complex geometric shapes and concepts, such as ellipses and spheres, and helps students develop spatial reasoning and problem-solving skills.

For a complete collection of terms related to Circles click on this link: Circles Collection.

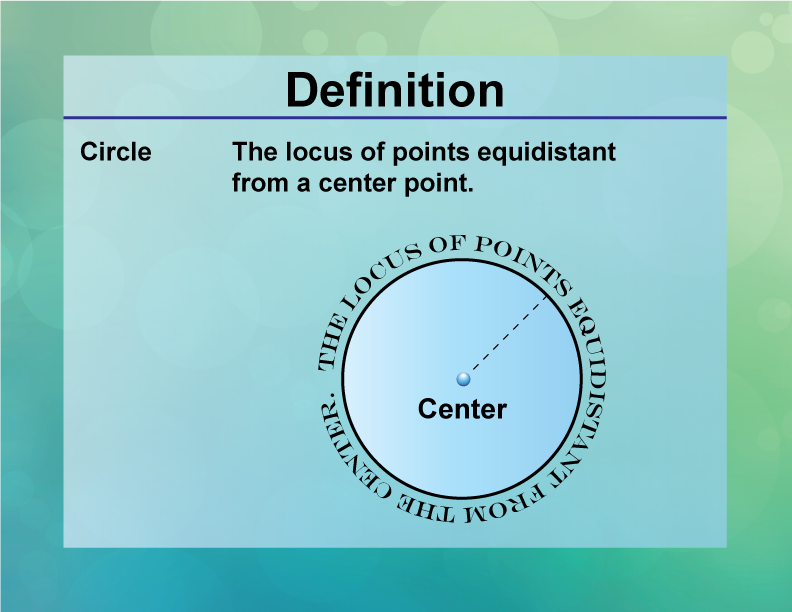
A circle is the locus of points equidistant from a given point, called the center. The "locus of points" are what you see as the circle.

The center is the one point not on the circular form. The distance from the center to any point on the circle is constant. This is part of the "locus of points" definition. The segment from the center to the circle is called the radius.

Since there are an infinite number of points that define the circle, then there are also an infinite number of radii (the plural of radius). This is shown below:

By contrast there is only one center point to the circle. A line segment that crosses the center and crosses the center is called a diameter. Think of a diameter as two collinear radii.

There is also the case of a line segment that intersects the circle at two points but does not cross the center. This is called a chord.

The diameter of a circle is a special type of chord. Do you see how the diameter also meets the definition of a chord?

When a line crosses a circle at two points, then it is a secant. 

When a line intersects a circle at just one point, then it is called a tangent line. 

A central angle is formed by two radii. The vertex of the angle is at the center of the circle.

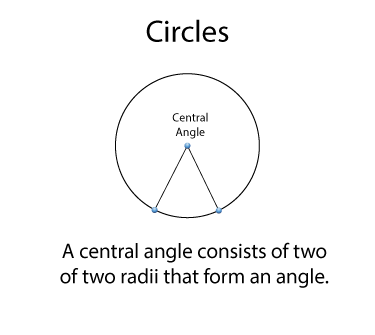
An inscribed angle is formed by two chords that intersect at the circle. Do you see where the vertex of the circle is located?

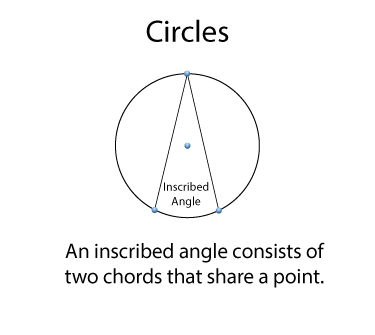
There is an important relationship between inscribed angles and central angles that share two points on the circle. In this case the inscribed angle is half the measurement of the central angle.

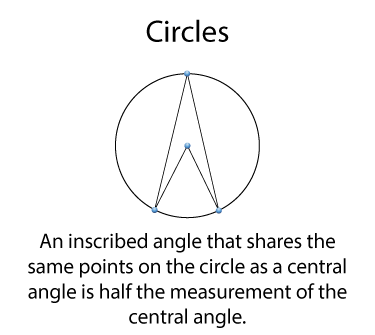
Using what we know about inscribed angles and diameters, then any inscribed angle of a diameter is a right angle. To see this, think of the diameter as a central angle of 180°.

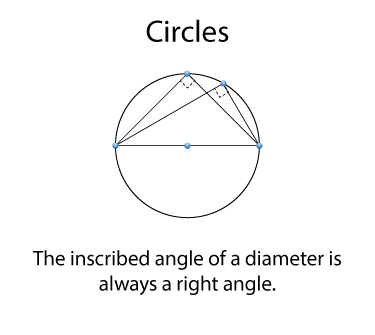
Finally, a line tangent to a circle is perpendicular to the radius of the circle at that point.