
Display Title
Closed Captioned Video: Percents: Fraction-Percent Conversion
Display Title
Closed Captioned Video: Percents: Fraction-Percent Conversion
Video Tutorial: Ratios: Fraction-Percent Conversion. In this video learn how to convert percents to fractions to simplify percent operations.
This video is part of a series of videos that cover the topic of percents. This includes the definition of a percent, percent operations, and applications of percents. Each video includes real-world examples of using percents to solve specific problems.
—CLICK ON PREVIEW TO VIEW THE VIDEO TUTORIAL—
To see the complete collection of video tutorials on percents, click on this link.
The following section provides background information on percents. Use this material to supplement the video series. You can also use the videos and this background material to fully review the topic of percents.
What Are Percents?
Percents are a type of fraction. A fraction is part of a whole.
When you think of fractions, you usually think of a numerical expression that looks like this:
A percent is a special type of fraction, as you can see here. When written as a fraction, a percent has a denominator of 100.
If you see a fraction with 100 in the denominator, think of it as a percent. In fact, the word “percent” literally means “out of 100.” An alternative to writing a percent as a fraction is to use the percent symbol, or %.
Converting Fractions to Percents
When comparing fractions, sometimes it's easier to convert them to percents. Take a look at these examples.

In each case, the denominator of the fraction isn't 100. Multiply the numerator and denominator by the same number to convert the denominator to 100. When you do that, you can write the fraction as a percent. The reason for multiplying the numerator and denominator by the same number is to not change the value of the fraction.
What if you have a fraction that isn't a factor of 100? In those case, you can divide the numerator by the denominator and multiply the result by 100%. Here's an example.
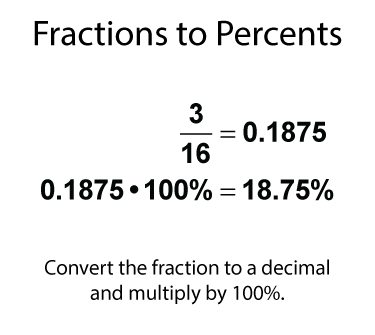
Why Convert Fractions to Percents?
When comparing fractions, sometimes it's easier to make these comparisons when the fractions are rewritten as percents. Take a look at this table, which lists fractions and their corresponding percent values.
| Fraction | Percent |
| 1/8 | 12.5% |
| 1/4 | 25% |
| 1/2 | 50% |
| 3/5 | 60% |
Do you see how much easier it is to compare and order fractions, if you are comparing the corresponding percent values?
Visual Models for Percents
You can use a visual model to represent percents. A 10 x 10 grid is made up of 100 smaller squares. Each small square represents 1%.
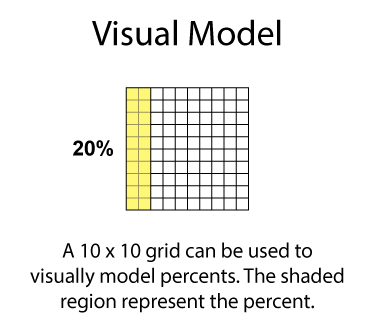
Visual models are useful when first learning about percents.
Percents as Decimals
You saw previously how fractions can be converted to decimals and then percents. Percents can also be represented as decimals.
Here's a way to convert a percent to a decimal using place value. Starting at the decimal point, shift it two places to the left and write the percent symbol. Here are several examples.

Use this technique when you need to find the percent of a number,
Percent of a Number
Since a percent is a type of fraction, then finding the percent of a number is the same as finding the fractional amount of a number. The simplest way to find the percent of a number is to multiply by the corresponding decimal value. Here are two examples.
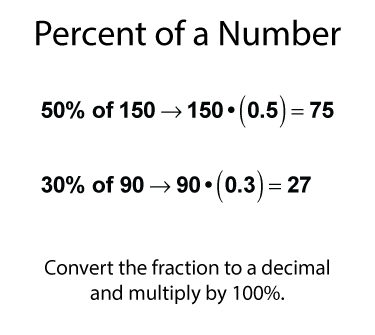
There are many examples of finding the percent of a number. One of the most common is the tax on a purchase. Suppose there's a 5% sales tax and you purchase a $25 item. What's the amount of tax owed? The calculation is shown below.
25 • 5% = 25 • (0.05) = 1.25
Percent Increase
When one number changes in value, that represents a percent change. For example, if you have money in a savings account and it earns interest, this is an example of percent increase. Here is the formula for calculating percent increase.

Suppose you bought a souvenir for $50 and resold it for $75. What is the percent increase in the value of the souvenir? Follow the steps for calculating the percent increase.

Percent Decrease
Suppose a number decreases in value. That also represents a percent change. In this case it is a percent decrease. Use the same formula to calculate the percent decrease.
Solving Percent Equations
Percents play an important role in solving equations. There are three types of equations that involve percents:
- Finding the percent of a number: x = a% • b.
- Finding the percent one number is of another: a • x% = b.
- Finding the whole given the percent: x • a% = b.
Study these three equation types and you'll be able to solve most problems that involve percents. As you solve word problems involving percents, you will likely be working with one of these equation types.
This is part of a collection of video tutorials on the topic of Percents.
To see the complete collection of the video tutorials on this topic, click on this link.
Note: The download is an MP4 video file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Video Library
To see the complete collection of math videos, click on this link.
Closed Captioned Video Library
This video is available in closed captioned format. To see the complete collection of captioned videos, click on this link.
Video Transcripts
This video has a transcript available. To see the complete collection of video transcripts, click on this link.
| Common Core Standards | CCSS.MATH.CONTENT.6.RP.A.3.C, CCSS.MATH.CONTENT.7.RP.A.1 |
|---|---|
| Duration | 3 minutes |
| Grade Range | 6 - 8 |
| Curriculum Nodes |
Algebra • Ratios, Proportions, and Percents • Percents |
| Copyright Year | 2020 |
| Keywords | percents, converting percents to fractions, video tutorial, Closed Captioned Video |