
These are the resources that support this Florida Standard.
MA.912.C.4.4 - Evaluate definite integrals by using the Fundamental Theorem of Calculus.
Displaying 1 - 50 of 88 resources:
| Thumbnail Image | Title | Description | Curriculum Nodes |
|---|---|---|---|
|
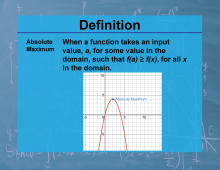
Definition--Calculus Topics--Absolute Maximum |
Definition--Calculus Topics--Absolute Maximum
When a function takes an input value, a, for some value in the domain, such that f(a) ≥ f(x), for all x in the domain. |
Calculus Vocabulary |
|
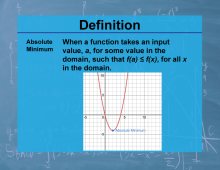
Definition--Calculus Topics--Absolute Minimum |
Definition--Calculus Topics--Absolute Minimum
When a function takes an input value, a, for some value in the domain, such that f(a) ≤ f(x), for all x in the domain. |
Calculus Vocabulary |
|
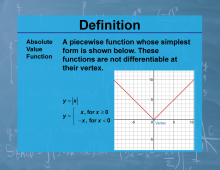
Definition--Calculus Topics--Absolute Value Function |
Definition--Calculus Topics--Absolute Value Function
A piecewise function whose simplest form is shown below. These functions are not differentiable at their vertex. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Acceleration |
Definition--Calculus Topics--Acceleration
The second derivative, with respect to time, for the displacement function. Acceleration is a vector quantity. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Antiderivative |
Definition--Calculus Topics--Antiderivative
For two differentiable functions f(x) and F(x), if F'(x) = f(x), then F(x) is the antiderivative of f(x). |
Calculus Vocabulary |
|
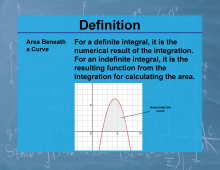
Definition--Calculus Topics--Area Beneath a Curve |
Definition--Calculus Topics--Area Beneath a Curve
For a definite integral, it is the numerical result of the integration. |
Calculus Vocabulary |
|
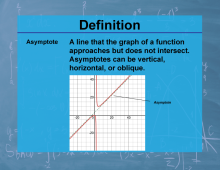
Definition--Calculus Topics--Asymptote |
Definition--Calculus Topics--Asymptote
A line that the graph of a function approaches but does not intersect. Asymptotes can be vertical, horizontal, or oblique. |
Calculus Vocabulary |
|
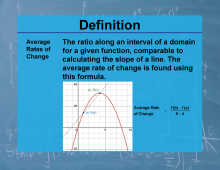
Definition--Calculus Topics--Average Rates of Change |
Definition--Calculus Topics--Average Rates of Change
The ratio along an interval of a domain for a given function, comparable to calculating the slope of a line. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Ceiling Function |
Definition--Calculus Topics--Ceiling Function
A discrete function that takes real number values and whose output is the least integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Chain Rule |
Definition--Calculus Topics--Chain Rule
The process for finding the derivative of a composite function. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Change of Variables |
Definition--Calculus Topics--Change of Variables
A substitution technique where a variable replaces a more complicated expression. In calculus it can simplify differentiation or integration. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Composite Function |
Definition--Calculus Topics--Composite Function
A function whose input values are made up of another function. For two functions f(x) and g(x), a composite function can be written as f(g(x)). |
Calculus Vocabulary |
|
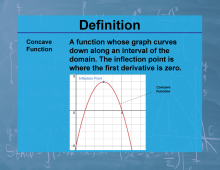
Definition--Calculus Topics--Concave Function |
Definition--Calculus Topics--Concave Function
A function whose graph curves down along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |
|
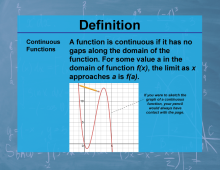
Definition--Calculus Topics--Continuous Functions |
Definition--Calculus Topics--Continuous Functions
A function is continuous if it has no gaps along the domain of the function. |
Calculus Vocabulary |
|
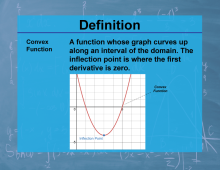
Definition--Calculus Topics--Convex Function |
Definition--Calculus Topics--Convex Function
A function whose graph curves up along an interval of the domain. The inflection point is where the first derivative is zero. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Definite Integral |
Definition--Calculus Topics--Definite Integral
The integral of a function with specific limits on the endpoints. A definite integral results in a numerical value. |
Calculus Vocabulary |
|
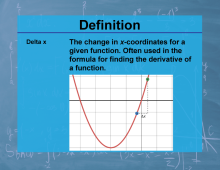
Definition--Calculus Topics--Delta x |
Definition--Calculus Topics--Delta x
The change in x-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |
|
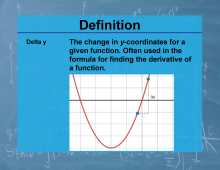
Definition--Calculus Topics--Delta y |
Definition--Calculus Topics--Delta y
The change in y-coordinates for a given function. Often used in the formula for finding the derivative of a function. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative |
Definition--Calculus Topics--Derivative
A function used to find the slope of a tangent to a curve at a given point. The derivative is based on the following limit. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Composite Function |
Definition--Calculus Topics--Derivative of a Composite Function
For two functions f(x) and g(x), the derivative of the composite function f(g(x)) is f'(x)*g'(x). This is an example of the Chain Rule. |
Calculus Vocabulary |
|
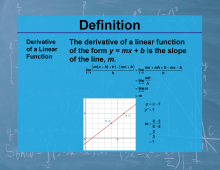
Definition--Calculus Topics--Derivative of a Linear Function |
Definition--Calculus Topics--Derivative of a Linear Function
The derivative of a linear function of the form y = mx + b is the slope of the line, m. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Logarithmic Function |
Definition--Calculus Topics--Derivative of a Logarithmic Function
The derivative of a logarithmic function uses the laws of logarithms and the definition of e to find the derivative. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Polynomial Function |
Definition--Calculus Topics--Derivative of a Polynomial Function
The derivative of a polynomial of degree n is another polynomial of degree n - 1. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Quadratic Function |
Definition--Calculus Topics--Derivative of a Quadratic Function
Since a quadratic function is a polynomial function of degree 2, the derivative is a linear function. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Rational Function |
Definition--Calculus Topics--Derivative of a Rational Function
Since a rational function is the ratio of two polynomials, the derivative of a rational function is also the ratio of two polynomials. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of a Trig Function |
Definition--Calculus Topics--Derivative of a Trig Function
The derivative of a trig function is another trig function, as shown in the table. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of an Exponential Function |
Definition--Calculus Topics--Derivative of an Exponential Function
The derivative of an exponential function is the product of the function and the natural log of the base. The derivative of ex is ex. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function |
Definition--Calculus Topics--Derivative of the Inverse of a Trig Function
Use implicit differentiation and the quotient rule to find the derivative of an inverse trig function. |
Calculus Vocabulary |
|
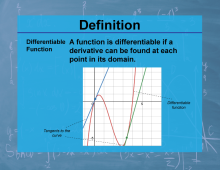
Definition--Calculus Topics--Differentiable Function |
Definition--Calculus Topics--Differentiable Function
A function is differentiable if a derivative can be found at each point in its domain. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Differential Equation |
Definition--Calculus Topics--Differential Equation
An equation that includes the derivative of a function f(x) and the variable x. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Differentiation |
Definition--Calculus Topics--Differentiation
The process of finding the derivative of a function. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Discontinuous Function |
Definition--Calculus Topics--Discontinuous Function
A function is discontinuous if it has one or more gaps along the domain of the function. The left- or right-hand limits exist but are not equal. |
Calculus Vocabulary |
|
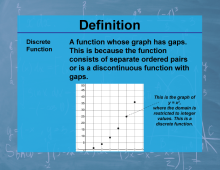
Definition--Calculus Topics--Discrete Function |
Definition--Calculus Topics--Discrete Function
A function whose graphs has gaps. This is because the function consists of separate ordered pairs or is a discontinuous function with gaps. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Displacement Function |
Definition--Calculus Topics--Displacement Function
A distance-vs.-time function used to find the distance an object has moved from a starting point. |
Calculus Vocabulary |

|
Definition--Calculus Topics--End Behavior |
Definition--Calculus Topics--End Behavior
The way a function f(x) changes as x approaches infinity, whether positive or negative. |
Calculus Vocabulary |
|
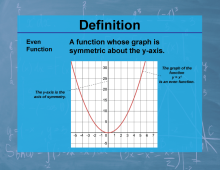
Definition--Calculus Topics--Even Function |
Definition--Calculus Topics--Even Function
A function whose graph is symmetric about the y-axis. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Explicit Function |
Definition--Calculus Topics--Explicit Function
A function in which y can be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equation. |
Calculus Vocabulary |
|
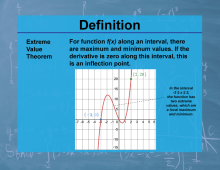
Definition--Calculus Topics--Extreme Value Theorem |
Definition--Calculus Topics--Extreme Value Theorem
For function f(x) along an interval, there are maximum and minimum values. If the derivative is zero along this interval, this is an inflection point. |
Calculus Vocabulary |
|
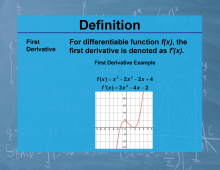
Definition--Calculus Topics--First Derivative |
Definition--Calculus Topics--First Derivative
For differentiable function f(x), the first derivative is denoted as f'(x). |
Calculus Vocabulary |

|
Definition--Calculus Topics--Floor Function |
Definition--Calculus Topics--Floor Function
A discrete function that takes real number values and whose output is the greatest integer value greater than the input value. The graph looks like a staircase. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Fundamental Theorem of Calculus |
Definition--Calculus Topics--Fundamental Theorem of Calculus
The theorem that relates differentiation and integration. The two operations are basically inverses of each other. |
Calculus Vocabulary |
|
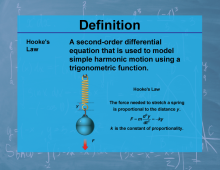
Definition--Calculus Topics--Hooke's Law |
Definition--Calculus Topics--Hooke's Law
A second-order differential equation that is used to model simple harmonic motion using a trigonometric function. |
Calculus Vocabulary |
|
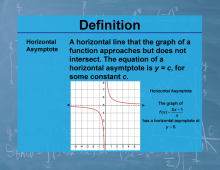
Definition--Calculus Topics--Horizontal Asymptote |
Definition--Calculus Topics--Horizontal Asymptote
A horizontal line that the graph of a function approaches but does not intersect. The equation of a horizontal asymptote is y = c, for some constant c. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Implicit Differentiation |
Definition--Calculus Topics--Implicit Differentiation
When a function cannot be written in the form of y as a function of x, then implicit differentation can be used to find the derivative with respect to x. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Implicit Function |
Definition--Calculus Topics--Implicit Function
A function in which y cannot be written as a function of x, where y is on the left side of the equation and all terms with x are on the right side of the equatio |
Calculus Vocabulary |

|
Definition--Calculus Topics--Indefinite Integral |
Definition--Calculus Topics--Indefinite Integral
The integral of a function without a specific limit on the endpoints. The result of an indefinite integral is a differentiable function. |
Calculus Vocabulary |
|
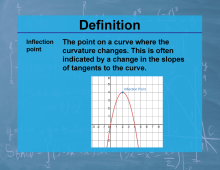
Definition--Calculus Topics--Inflection Point |
Definition--Calculus Topics--Inflection Point
The point on a curve where the curvature changes. This is often indicated by a change in the slopes of tangents to the curve. |
Calculus Vocabulary |
|
Definition--Calculus Topics--Instantaneous Rate of Change |
Definition--Calculus Topics--Instantaneous Rate of Change
Another way of describing the slope of the line tangent to a given curve at a given point. |
Calculus Vocabulary |

|
Definition--Calculus Topics--Integral |
Definition--Calculus Topics--Integral
A method for finding the area of a curve along an interval. In calculus, integrating a function f(x) involves finding the antiderivative of f(x). |
Calculus Vocabulary |

|
Definition--Calculus Topics--Integral Symbol |
Definition--Calculus Topics--Integral Symbol
The mathematical symbol used to denote the process of integration. |
Calculus Vocabulary |