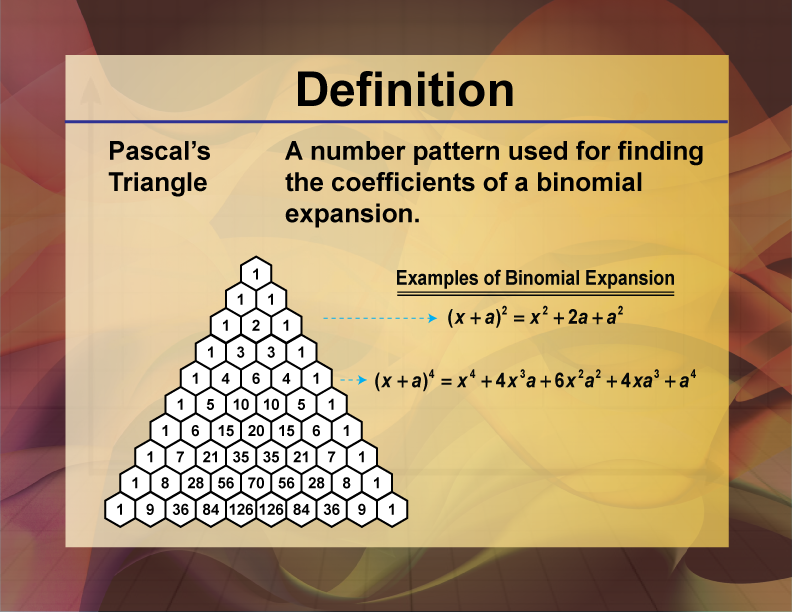
Video Definition 26--Polynomial Concepts--Pascal's Triangle
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Polynomials >> Polynomial Expressions

Video Definition 26--Polynomial Concepts--Pascal's Triangle

Video Definition 26--Polynomial Concepts--Pascal's Triangle

Topic

Polynomials

Description

Pascal’s Triangle: A number pattern used for finding the coefficients of a binomial expansion. Example: (x + a)4 = x4 + 4x3a + 6x2a2 + 4xa3 + a4. Provides the foundational definition of a polynomial, essential for understanding the topic.

Polynomials are foundational to algebra, representing expressions with one or more terms. These terms are composed of variables raised to various powers and coefficients. Understanding their structure and function allows mathematicians to model real-world situations effectively. This video elucidates such concepts clearly.

Teacher’s Script: Let's delve into polynomials today! These mathematical expressions allow us to represent complex relationships with simple terms. The video you'll watch explores this idea in depth, focusing on how each term contributes to the polynomial's behavior. Pay attention to the examples provided; they show how to break down and understand these expressions step-by-step.

For a complete collection of videos related to Polynomials click on this link: Math Video Definitions: Polynomials Collection.

Common Core Standards CCSS.MATH.CONTENT.HSA.APR.A.1, CCSS.MATH.CONTENT.HSA.APR.B.2, CCSS.MATH.CONTENT.HSA.APR.C.5, CCSS.MATH.CONTENT.HSA.APR.C.4, CCSS.MATH.CONTENT.HSA.APR.B.3, CCSS.MATH.CONTENT.HSF.IF.C.7.C
Duration 1 minutes
Grade Range 8 - 12
Curriculum Nodes Algebra
    • Polynomials
        • Polynomial Expressions
Copyright Year 2024
Keywords polynomials, monomials, definitions, glossary term, Pascal's Triangle