Display Title
Math Clip Art--Linear Function Tables 10
Display Title
Math Clip Art | Linear Function Tables 10
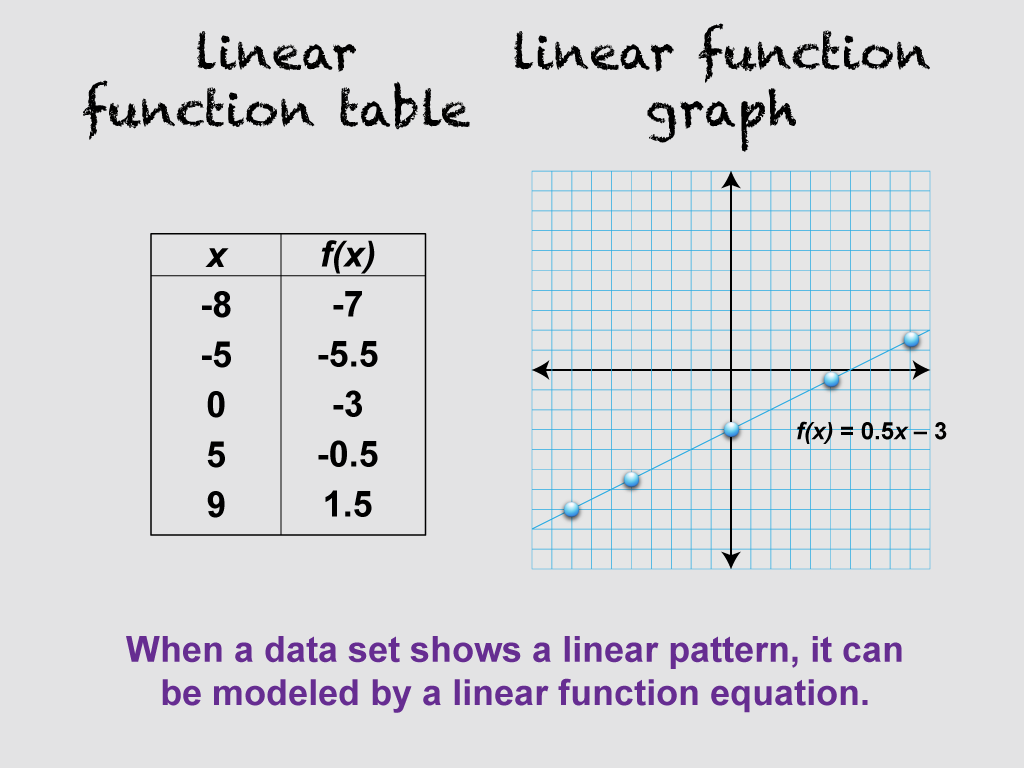
This is part of a collection of clip art images showing linear functions in tabular form. These downloadable images are easily incorporated into a lesson plan.
—CLICK PREVIEW TO SEE THE CLIP ART IMAGE—
To see the complete collection of clip art images on this topic, click on this link.
The following section reviews linear expressions, equation, and functions. Use this section to review these key concepts.
Linear Expressions, Equations, and Functions
Linear Expressions
Linear expressions include a variable whose exponent is 1. Here are some examples of linear expressions:
Be sure you know how to translate a verbal expression into a linear expression like the ones shown above. To see examples of how to do this, click on this link to see a slide show.
Expressions aren’t equations but they are an important component of linear equations. Also, you can add and subtract linear expressions and still have a linear expression. Multiplying or dividing linear expressions will result in a non-linear expression. Here are some examples:
Interpreting ExpressionsExample 1 It costs $24/hour to rent a bike and the total fee is summarized by this expression: Questions you might be asked:
Example 2 A hollow tube of radius r and length l is flattened into a rectangle. What is the perimeter of this rectangle? Perimeter is based on the linear expression 2(l + w), where l is the length of the rectangle and w is the width. Find the corresponding expressions for these terms from the diagram. The length of the rectangle corresponds to the circumference of the circular part of the cylinder. The width of the rectangle corresponds to the height of the cylinder. The resulting perimeter expression is this: |
Linear Equations
Linear equations include a linear expression equal to a number or another linear expression. A linear equation can have one or more variables, but all terms must be linear.
Here are examples of linear equations with one variable.
Solving EquationsExample 1 This is a one-variable equation with fractions. Start by isolating the x-term on the left side of the equation: Then multiply both sides by 3 to isolate x on the left, and simplify to solve. Example 2 Interpret the verbal description to write the equation: Now solve for x: Recall that the question asked for 10x: |
If you need more practice in solving one-variable equations, click on the following links:
- Solving One-Step Addition Equations
- Solving One-Step Subtraction Equations
- Solving One-Step Multiplication Equations
- Solving One-Step Division Equations
- Solving Two-Step Multiplication and Addition Equations
- Solving Two-Step Multiplication and Subtraction Equations
- Solving Two-Step Division and Addition Equations
- Solving Two-Step Division and Subtraction Equations
Another skill related to equation solving is the ability to rewrite an equation in an equivalent form. See the examples below.
Manipulating EquationsExample 1 Suppose 3x = 27, what is the value of 12x ÷ 6? To get the expression 12x on the left side of the equation, multiply both sides by 4. Next divide both sides by 6: Example 2 Suppose 12x = 48, what is the value of 15x + 10? To get the expression 15x solve for x and multiply by 15: Now add 10 to both sides of the equation: |
Make sure you are comfortable with the properties of equality and the structure of an equation. For a quick review, click on this link.
Linear Functions
Before studying what a linear function is, make sure you are comfortable with the following concepts, which we will also review:
- What a function is
- Independent variable
- Dependent variable
- Domain
- Range
- Different representations of functions
Brief Review of Functions
What Is a Function? A function is a one-to-one mapping of input values (the independent variable) to output values (the dependent variable). Click on this link to see a quick tutorial on what a function is. This slide show goes over the following key points:
- For every input value (x), there is a unique output value, f(x).
- Functions can be represented as equations, tables, and graphs.
- A function machine is a useful visual representation of the input/output nature of functions.
Dependent/Independent Variables. When one variable depends on another, then it is the dependent variable. For example, the faster your speed, the farther you travel. Suppose that speed is represented by the variable s and the distance traveled is represented by the variable d.
Here’s how to describe the relationship between s and d:
The faster the speed, the more distance traveled.
Distance is dependent on speed.
Distance is a function of speed.
d = f(s)
When studying functions, make sure you are comfortable telling the difference between the independent variable and dependent variable. Get comfortable using function notation. To learn more about function notation, click on this link.
Domain and Range. A function shows the relationship between two variables, the independent variable and the dependent variable. The domain is the allowed values for the independent variable. The range is the allowed values for the dependent variable. The domain and range influence what the graph of the function looks like.
For a detailed review of what domain and range are, click on this link to learn more. You’ll see definitions of the terms domain and range, as well as examples of how to find the domain and range for given functions.
Multiple Representations of Functions. We mentioned previously that functions can be represented in different ways. In fact, any function can be represented by an equation, usually f(x) equal to some expression; a table; or a graph. For a detailed review of multiple representations of functions, click on this link, to see a slide show that includes examples of these multiple representations.
Slope-Intercept Form
The most important form of a linear function is the slope-intercept form.
Given the slope, m, and the y-intercept, b, for a linear function, you can easily construct the equation and graph of the linear function. To see examples of graphing linear functions in slope-intercept form, click on this link. This slide show also includes a video tutorial.
Point-Slope Form
Another method of finding the slope-intercept form involves using the point-slope form. In this case you are given the slope, m, of the line and one set of coordinates, (x, y), on the line. This is what the point-slope form looks like.
To see examples of deriving the linear function using the in point-slope form, click on this link. This slide show tutorial walks you through the process and provides several worked-out examples.
A number of SAT questions will test your understanding of linear functions in slope-intercept and point-slope form.
Deriving a Linear FunctionThese examples rely on a basic understanding of slope-intercept form. Example 1 What is the slope-intercept form of the equation of this graph? You can see from the graph that the y-intercept is 2. To determine the slope of the line, follow these steps:
For this graph the slope is 4/1, or 4. The equation in slope-intercept form is this: Example 2 A line with a slope of 2 passes through the origin and through the point (k, 10). What is the value of k? A line that passes through the origin has a slope intercept of zero. This is the slope-intercept form. Now input the coordinates (k, 10) to find the value of k: Example 3 A line with a slope of -3 and y-intercept of 2 passes through the origin and through the point (k, 5). What is the value of k? Write the equation in slope-intercept form: Now input the coordinates (k, 5) to find the value of k: Example 4 The line y = kx +3, where k is a constant, passes through the point (c, d). What is the slope of the line in terms of c and d? In this case you’re given the equation in slope-intercept form. Simply plug in the values of c and d to find the value for k, which is the slope. Example 5 A line passes through the origin, as well as the points (3, k) and (k, 12). What is a possible value of k? A line that passes through the origin has a slope intercept of zero. This is the slope-intercept form. Plug in the two sets of coordinates to get two separate equations: Now plug in the expression for k in the second expression and solve for m: There are two possible values for m, and, therefore, two separate values for k. This is one possible slope-intercept form with the one of the values for m: Plug in one of the coordinates to solve for k: |
Slope-Based Questions
First, let’s review the basics of slope. This is the slope formula:
Given two coordinates, the slope of the line connecting the two points is found using the slope formula.
The key to understanding this is the slope-intercept form for parallel and perpendicular lines. Review these definitions:
Basically, lines that are parallel have the same slope. Lines that are perpendicular have slopes that are negative reciprocals. Look at the following examples.
To see examples of finding the equations of parallel and perpendicular lines, click on the following links:
|
Slope-Based Questions These examples rely on a basic understanding of slope. Example 1 The graph of a linear equation is 8x - 2y = 120. Decide if the graph of 3x + 5y = 150 is perpendicular to this line. Write both equations in slope-intercept form: These slopes are not inverse reciprocals of each other. A line perpendicular to y = 4x - 60 would have a slope of -¼. A line perpendicular to y = -6x + 30 would have a slope of ⅙. These lines are not perpendicular to each other. Example 2 The graph of a linear equation is -4x + 3y = 48. What is the equation of the line through (-1, 4) that is perpendicular to this line? Write the equation in slope-intercept form: A line perpendicular to this line would have a slope of -¾. Use the point-slope form to find the line that crosses (-1, 4): |
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math clip art on this topic. To see the complete clip art collection, click on this link.
To learn more about Slide Show Creator, click on this Link:
Accessibility
This resource can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.8.F.A.2, CCSS.MATH.CONTENT.8.F.A.3, CCSS.MATH.CONTENT.HSF.LE.A.1.A |
|---|---|
| Grade Range | 8 - 10 |
| Curriculum Nodes |
Algebra • Linear Functions and Equations • Graphs of Linear Functions • Slope-Intercept Form |
| Copyright Year | 2021 |
| Keywords | linear functions, Proportional |