Display Title
Math Clip Art--Base Ten Blocks--52
Display Title
Math Clip Art--Base Ten Blocks--52
This is a collection of clip art images that you can use to model different numbers. This complete collection models two- and three-digit numbers using base 10 blocks. To see the complete collection of these clip art images, click on this link.
— CLICK THE PREVIEW BUTTON TO SEE THE CLIP ART IMAGE —
The following review provides basic information about place value.
The Base 10 Number System
When you first learned to count, you started at zero or one and counted to nine.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
After nine, the numbers started repeating.
10, 11, 12, 13, 14, 15, 16, 17, 18, 19
After 19, the pattern of numbers continues. In fact, counting numbers involves just using the digits from 0 to 9 in different combinations.
Why is that?
Our numbering system is called a base 10 system. This means there are ten digits, which you know as 0 to 9. All numbers in a base 10 system just use these digits.
Counting in a Base 10 System
When you look at a number, each digit represents a certain place value. Take a look at this three-digit number
The digit 3 is in the ones place. The digit 2 is in the tens place. The digit 1 is in the hundreds place.
The digit 3 is in the ones place. The digit 2 is in the tens place. The digit 1 is in the hundreds place.
For whole numbers, place value increases 10-fold.
Place Value in the Base 10 System
Place value determines the size of a number. Take a look at this number:
23
In the ones place is the digit 3, but int he tens place is the digit 2. Don't let the single digit fool you. The 2 in the tens place has a value of 20.
Now look at this number:
542
In the ones place is the digit 2. In the tens place is the digit 4. In the hundreds place is 5. If we were to separate these numbers, we would see this:
500
40
2
So, in going from left to right starting at the decimal point, each place value is ten times the value of the place value to the right.
If you're given a description of a number using just place value information, you can write a number. Here's an example.
The digit in the ones place is 5. The digit in the tens place is 3. The digit in the hundreds place is 9. What is the number?
Using this description we write the following number: 935.
Number Systems with Other Bases
You've seen how the base 10 number system works, but why do we use a base 10 system? Are there other number systems?
Let's address the first question. The reason we use a base 10 system is probably because we have ten fingers to count with. Do you think it's a coincidence that our base 10 numbering system aligns with our 10 fingers to count?
But we have 10 fingers and 10 toes. Are there number systems that use base 20. Yes!
The Mayan culture used a base 20 system for counting. These are twenty symbols used to count.
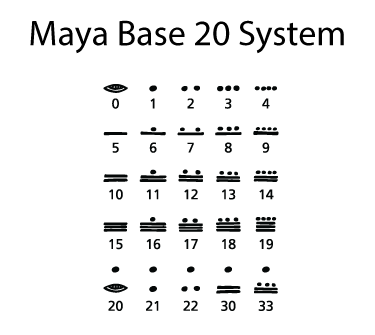
This numbering system uses just three symbols in different combinations: dots, dashes, and the shell. The shell represents zero. The dash represents an increment of five. The dot represents a value of one. Different combinations of these symbols can model any number.
Another, even more popular system is the binary system, which is used extensively with computers. With the binary system, there are only two digits: 0 and 1. This combination of digits can be used any number equivalent to our base 10 numbers. Here are the first 10 numbers in binary and base 10.
| Base 10 | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Why do computers use a binary, or base 2, system? What is the advantage of a binary system?
Computer circuitry and connections involve a lot of on-off switching. Many computer commands are basically combinations of these on-off switches. A binary system is ideal for modeling an on-off system. If you let 0 mean off and 1 mean on, then a binary code can be used to model not only numbers but any computer state.
Each number system has its own rules for writing numbers. Once you learn the rules, then you can write any number in any number system.
Number Models: Base Ten Blocks
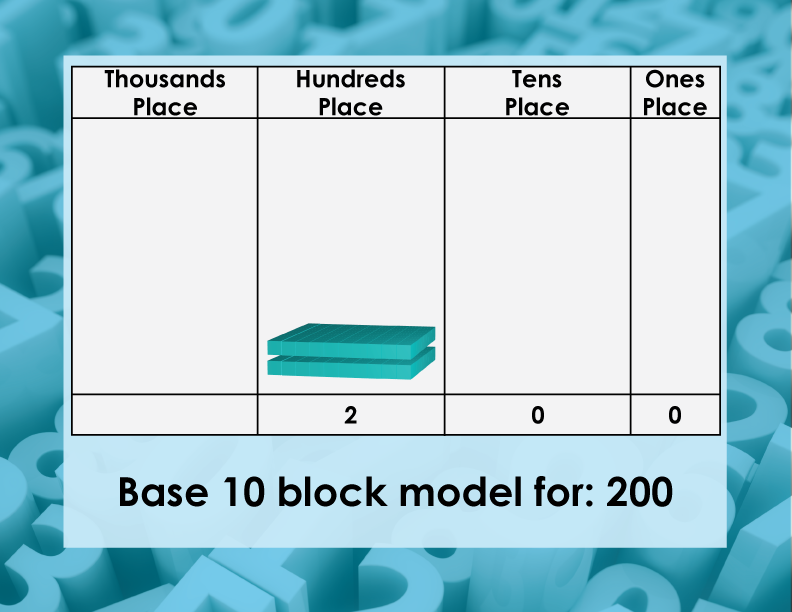
One way to model base ten numbers is to use number models, and one of the best ones to use is to use base ten blocks. Base ten blocks are a visual model to represent numbers. Here is what these models look like.
For each of these models, place the correct number of blocks to model the digit in that place value.
This is a model for the number 24. There are two tens blocks in the tens place and four ones blocks in the ones place.
Here is a number to the hundreds place.
To model 250, put two hundreds blocks in the hundreds place, five tens blocks in the tens place, and no blocks in the ones place.
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math clip art on this topic. To see the complete clip art collection, click on this Link.
To learn more about Slide Show Creator, click on this Link
Accessibility
This resource can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.K.NBT.A.1, CCSS.MATH.CONTENT.1.NBT.B.2, CCSS.MATH.CONTENT.2.NBT.A.1 |
|---|---|
| Grade Range | K - 3 |
| Curriculum Nodes |
Arithmetic • Numbers and Patterns • Place Value |
| Copyright Year | 2021 |
| Keywords | place value, base ten blocks |