Display Title
Formulas--Area of a Right Triangle
Display Title
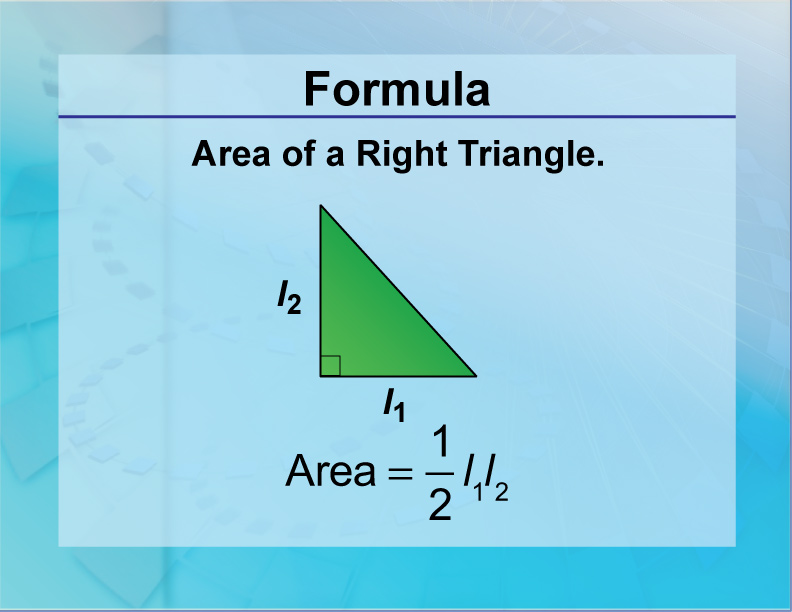
Area of a Right Triangle
This is the formula for finding the area of a right triangle. This is part of a collection of resources that include key math formulas.
—CLICK ON THE PREVIEW BUTTON TO SEE THE IMAGE—
To see the complete collection of formulas, click on this link.
The following section provides background information on right triangles and area.
Brief Review of Right Triangles
A right triangle has certain properties regarding its angles and sides. A right triangle has a right angle and two acute angles. The right angle gives the right triangle a distinctive square corner.

The sides of the triangle that define the right angle are called the legs of the triangle. The sides are vertical and horizontal. The third side, called the hypotenuse, is slanted.

Any triangle can be divided into two right triangles that share a side. Here are two examples.
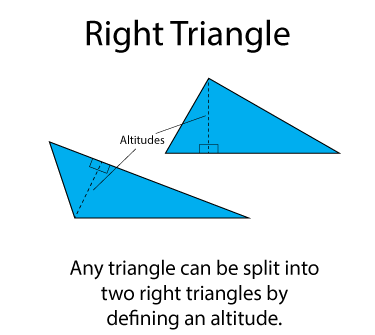
Notice how the altitude starts at one of the vertices and intersects the side opposite the vertex at a ninety-degree angle. This altitude of a triangle is important when calculating the area of the triangle.
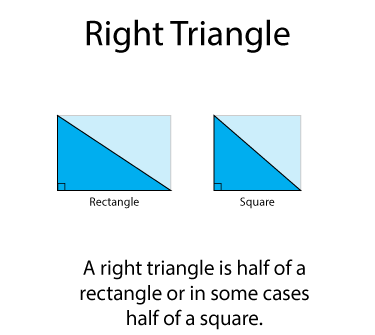
A right triangle is half a rectangle, or in some cases have a square. In the illustration below, each right triangle is next to a congruent version of itself. In each case a rectangle or square is formed.
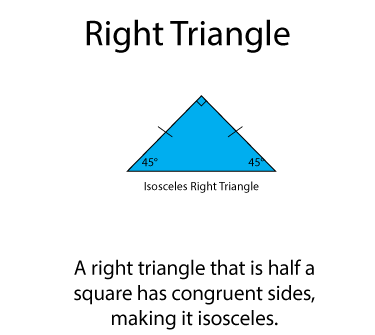
In the case of the square, the right triangle has two congruent sides, making it an isosceles right triangle. Notice that the congruent angles are each 45°.
Because of this property of right triangles, then any triangle can be considered half of a rectangle. Here is an example of this.

This is an important concept when finding the area of a triangle.
Brief Review of Area
Area is the amount of two-dimensional space that a geometric shape takes up.
With simple geometric shapes the area is usually the product of two numbers that represent side lengths. For example, here is a rectangle.
To find the area of this rectangle, multiply the length of the base and height of the rectangle.
Area of a Triangle
The idea of multiplying the base and height also applies to triangles. Here is the formula for finding the area of a triangle.
Notice that the height is perpendicular to the base. The area of a triangle is half the area of the corresponding rectangle formed from the base and height lengths.
In the case of a right triangle, finding the area of it is a variation of the standard formula for finding the area of any right triangle.
Special Right Triangles
In the case of an isosceles right triangle, the area is equivalent to the half the area of the corresponding square.
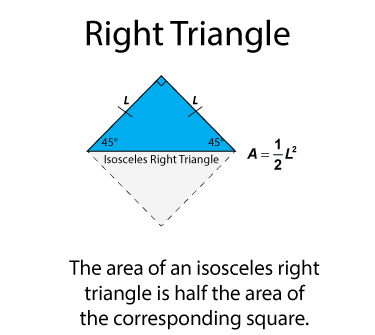
Notice that the area for an equilateral right triangle has a squared term. That's because the lengths of the legs of such triangles are congruent.
Certain right triangles have a ratio between the two legs that allows you to find the area quickly. Take a look at this 30°-60°-90° right triangle. Notice the ratio of the legs for triangles of this configuration.

So, any 30°-60°-90° right triangle maintains this ratio of the legs, as shown in this illustration.

So, if you have a 30°-60°-90° right triangle, the area is going to be the square root of the 3 times the length of the base squared. For example, a 30°-60°-90° with a base length of 10 has an area of 100 times the square root of 3.
Here's another special right triangle.

A right triangle that has these side lengths, or a ratio of these side lengths, then you can easily find the area of the right triangle.
Here's a right triangle that's proportional to a 3-4-5 right triangle. Its area is easily calculated.

Here's another way of looking at these right triangles. Suppose a right triangle is proportional to a 3-4-5 triangle by a factor of s. Use this formula to find the area for such a triangle.

Here's another special right triangle. This one has side length ratios of 5:12:13, as shown below.

As we did with the other special right triangle, you can create a formula for finding the area of any right triangle proportional to the 5:12:13 triangle.

The downloadable image is part of a collection of images that represent different math formulas.
Related Resources
To see the complete collection of Formulas, click on this link.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math formulas and definitions on this topic. To see the complete collection of definitions, click on this Link.
To learn more about Slide Show Creator, click on this Link:
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.6.G.A.1 |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Geometry • Triangles • Area and Perimeter of Triangles |
| Copyright Year | 2013 |
| Keywords | area, triangle, formulas |