Display Title
Definition--Triangle Concepts--Triangle, Definition 1
Display Title
Triangle, Definition 1

Topic
Triangles
Definition
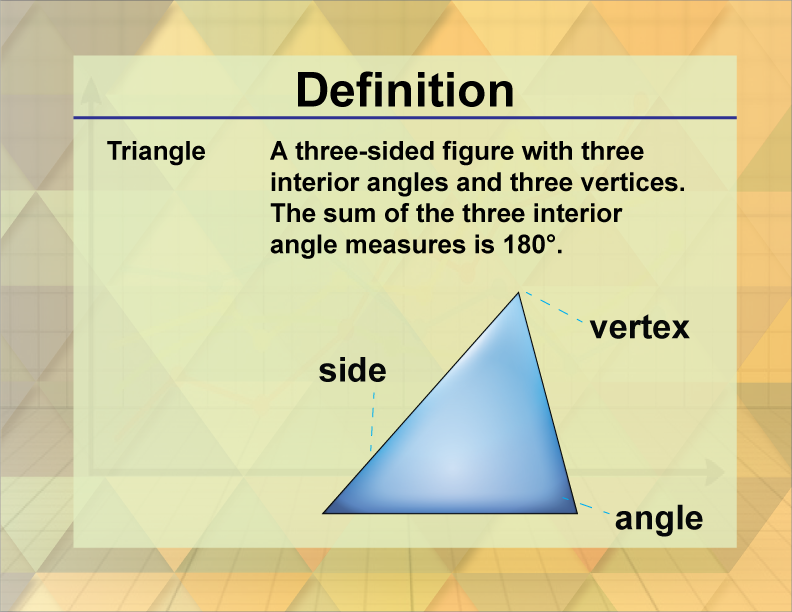
A triangle is a polygon with three edges and three vertices.
Description
A triangle is one of the simplest and most fundamental shapes in geometry, characterized by having three sides and three vertices. The sum of the interior angles of a triangle is always 180 degrees, which is a key property used in various geometric proofs and constructions.
In real-world applications, triangles are used extensively in engineering, architecture, and design due to their inherent stability and strength. For example, triangular structures are often used in bridges and roof trusses to distribute weight evenly and provide support.
In math education, understanding the basic properties of triangles is essential for students to grasp more complex geometric concepts. Triangles serve as the building blocks for more advanced shapes and are used in various mathematical problems and proofs. By mastering the properties of triangles, students can develop a deeper understanding of geometry and its applications.
For a complete collection of terms related to functions and relations click on this link: Triangles Collection
Watch this video to learn about triangles. The video shows you how to use the Desmos geometry tools to create and explore triangles. (The transcript is also available.)
Video Transcript
In this tutorial, we define and explore the properties of triangles using the Desmos geometry tools.
Let’s start by creating a closed figure. Start with a point. Create a line segment. From the endpoint of that line segment create another line segment. Continue adding line segments until you end up at the original point. This is a closed figure.
In this case a series of coplanar segments that start and end at the same point. A closed figure can also consist of curved sides.
A triangle is a closed figure. A triangle has three sides made up of three line segments. See the three segments that make up this triangle? Each endpoint of the segments can be labeled.
This is triangle ABC. Use the labels to define the sides of the triangles. Triangle ABC has sides AB, BC, and AC. Each of those sides is a line segment.
A triangle consists of three angles. There are three angles: Angle CAB, angle ABC, and angle CBA.
So you can see how the endpoints of the segments define the sides and angles. The endpoints can also be used to label the sides and angles. Point A is the vertex of angle A. The side opposite angle A is side a. Point B is the vertex of angle B. The side opposite angle B is side b. Point C is the vertex of angle C. The side opposite angle C is side c. Finally the sum of the angles of a triangle is 180°.
Let’s explore triangles using the Desmos geometry tools.
There are two ways to construct a triangle. Here’s one way.
From the geometry window, click on the Segment tool. Click once to define one of the endpoints. Move to another part of the screen and click again. Here is a segment that will be one of the sides of our triangle.
Start the second segment at the endpoint of the first segment. Make sure the cursor is right over this endpoint. Click once and move to a different part of the screen. Click again to define the second segment. You can see the triangle taking shape.
In fact, the endpoints of the third side are already there. Click from one endpoint to another to define the third side. Click on the selection tool to select and move the points. Try to get your triangle to look like this.
Label the points. Click on each point and select the label option. Try to get your triangle to look like this.
Measure the angles. Click on the Angle tool. Measure each angle by clicking on the three points that define the angle. You’ll see the angle measures for all three angles. Add the three angles to verify that they add up to 180 degrees.
Change the size and shape of the triangle. You’ll see different angle measures, but they should add up to 180 degrees.
Now let’s look at the other way of constructing a triangle. Click on the Polygon tool. Click once and move to a different point on the screen. Click again. Move to a third point. Click again. Finally, click on the original point. You should see a second triangle.
Label the triangle, and measure the angles. Manipulate this triangle to verify that the sum of the three angles is 180 degrees.
Definition of a Triangle
A triangle is a closed figure that has three sides made up of three line segments.
See the three segments that make up this triangular shape?
Each endpoint of the segments can be labeled. This is triangle ABC.
Use the labels to define the three sides. Triangle ABC has sides AB, BC, and AC. Each of those sides is a line segment.
A triangle consists of three angles. There are three angles: Angle CAB, angle ABC, and angle CBA. So you can see how the endpoints of the segments
define the sides and angles.
The endpoints can also be used to label the sides and angles. Point A is the vertex of angle A. The side opposite angle A is side a. Point B is the vertex of angle B.
The side opposite angle B is side b. Point C is the vertex of angle C. The side opposite angle C is side c. Finally the sum of the angles of a triangle is 180°.
Types of Triangles
Depending on the angle measures and side lengths, different types of triangles can be formed. Here are triangles classified by angle measure:
- Acute. A triangle whose three angles are acute angles. Acute angles measure less than 90 degrees.
- Obtuse. A triangle that has one angle that’s obtuse. Obtuse angles measure greater than 90 degrees. The other two angles of the triangle are acute.
- Right. A triangle that has a right angle. Right angles measure 90 degrees. The other angles of the triangle are acute.
- Equiangular. A triangle whose angles are all congruent. Each angle measures 60 degrees.
Here are triangles classified by side length:
- Scalene. A triangle that has three sides of different lengths.
- Isosceles. A triangle that has two congruent sides.
- Equilateral. A triangle whose side lengths are all congruent. An equilateral triangle is also an equiangular triangle.
To learn more about triangles, click on each of the slide shows below:
Applications of Triangles
Applications of triangles are found in many natural and man-made objects. Watch this video to learn about applications in architecture.
Video Transcript
THE BANK OF CHINA TOWER IN HONG KONG IS STYLISH AND STRONG.
SKYSCRAPERS BUILT HERE HAVE TO WITHSTAND STRONG WINDS DURING TYPHOON SEASON.
THE ARCHITECT OF THE BANK OF CHINA TOWER, I.M. PEI, RELIED ON THE USE OF A STRONG TRIANGULAR BASE TO REINFORCE THE TOWER.
ARCHITECTS USE TRIANGULAR SHAPES TO HELP STRENGTHEN BUILDINGS.
BUT WHAT IS IT ABOUT TRIANGLES THAT MAKES FOR GOOD ARCHITECTURAL SUPPORT?
WHY AREN'T RECTANGLES OR OTHER POLYGONS AS USEFUL?
WHILE SQUARES, POLYGONS AND CIRCLES ARE OFTEN USED BY ARCHITECTS, THE TRIANGLE HOLDS A SPECIAL PLACE WHEN IT COMES TO SUPPORT.
IN THIS PROGRAM YOU WILL EXPLORE THE PROPERTIES OF TRIANGLES AND YOU WILL SEE HOW THESE PROPERTIES ARE USED TO SOLVE REAL-WORLD PROBLEMS.
IN PARTICULAR, THE FOLLOWING CONCEPTS ARE EXPLORED:
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.1, CCSS.MATH.CONTENT.7.G.A.2, CCSS.MATH.CONTENT.4.G.A.2 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Triangles • Definition of a Triangle |
| Copyright Year | 2021 |
| Keywords | triangle, defnitions, glossary |