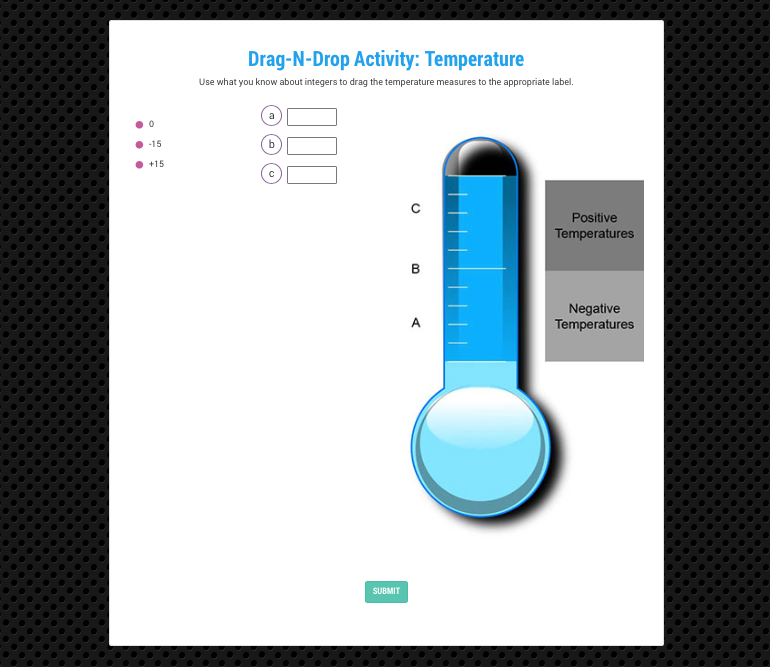
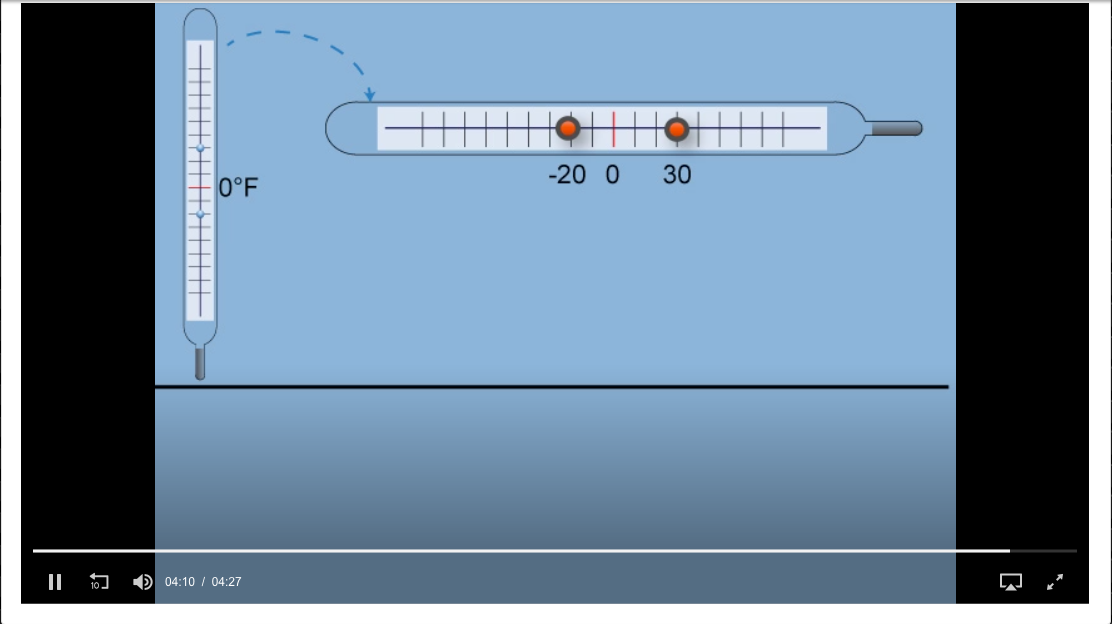
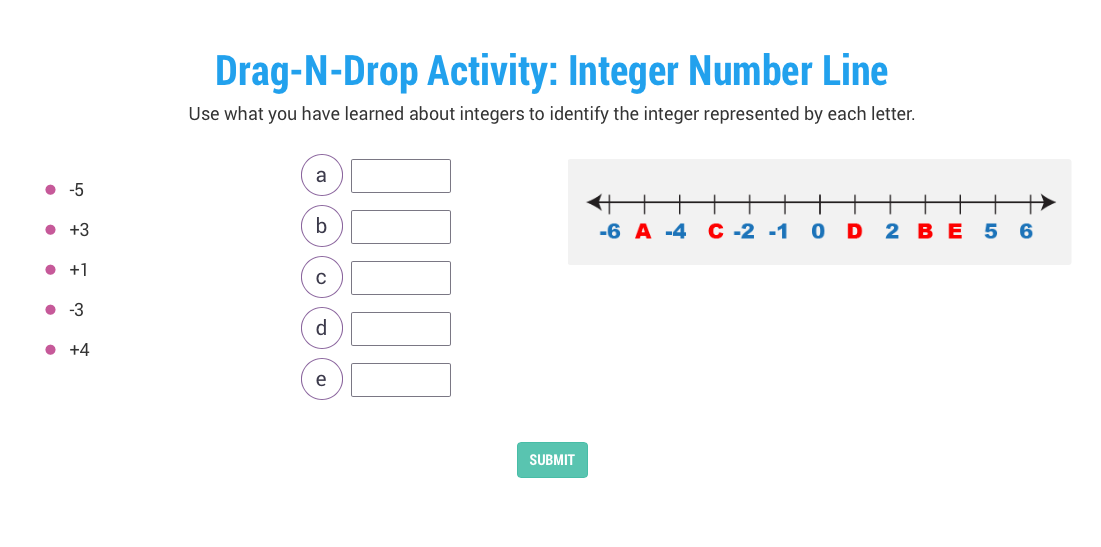
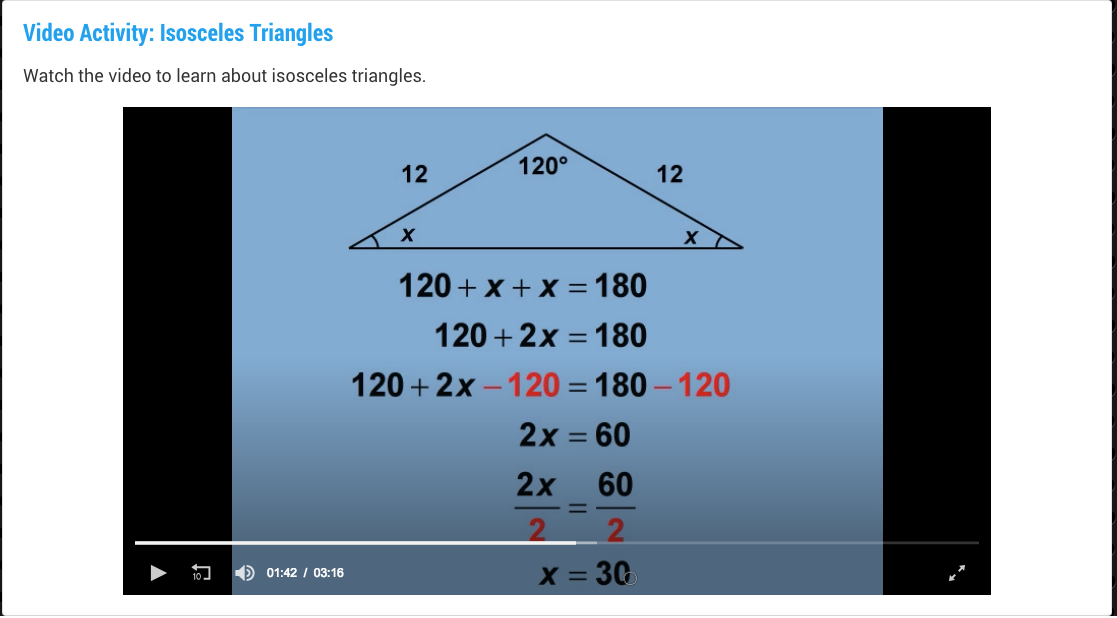
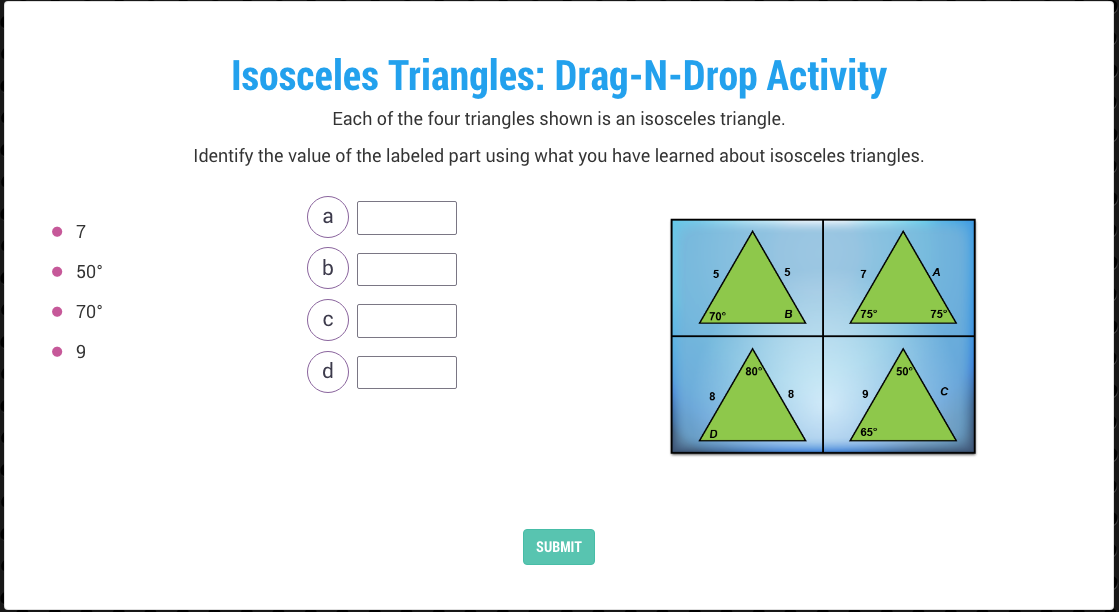
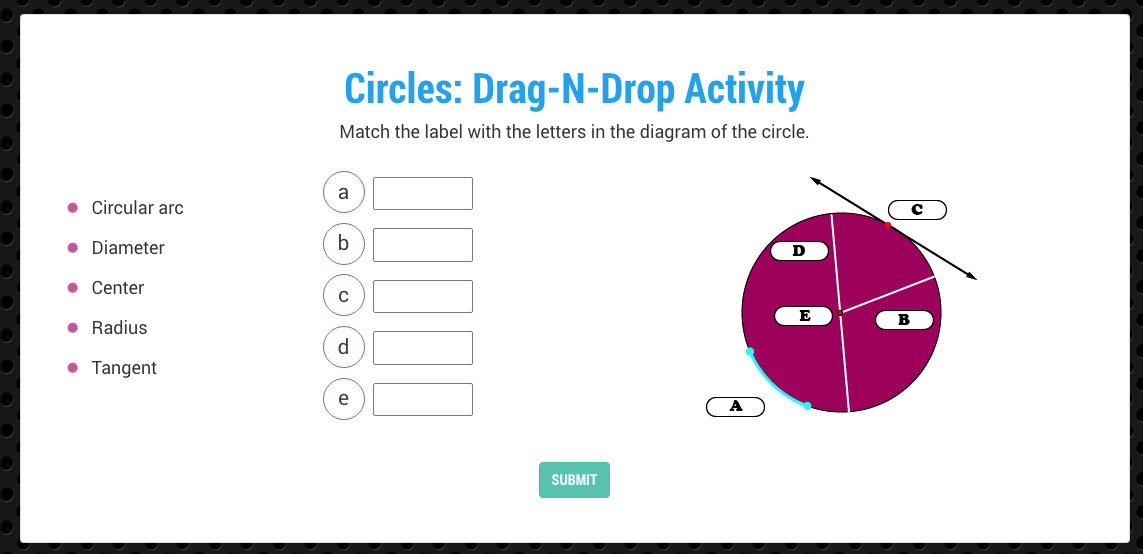
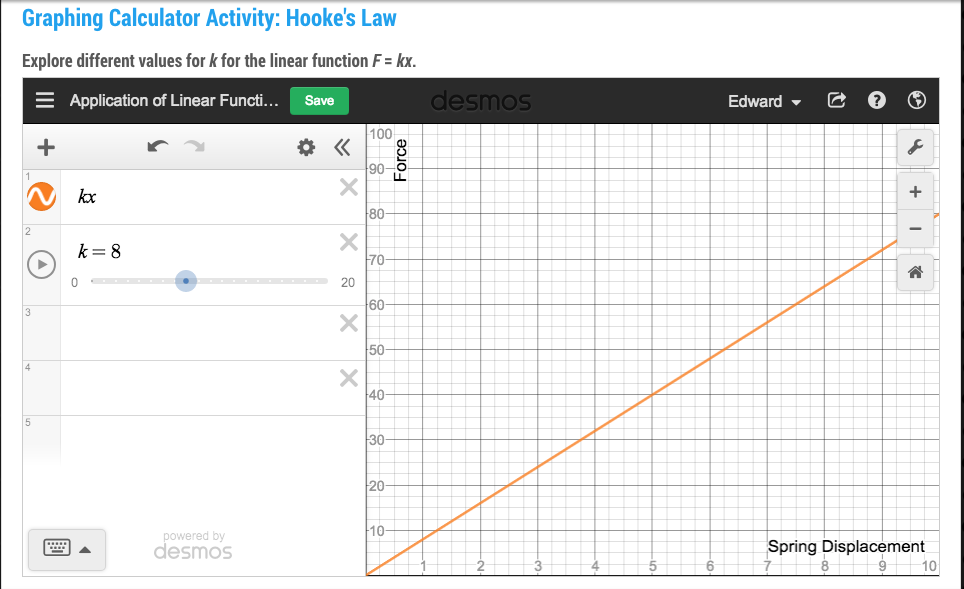
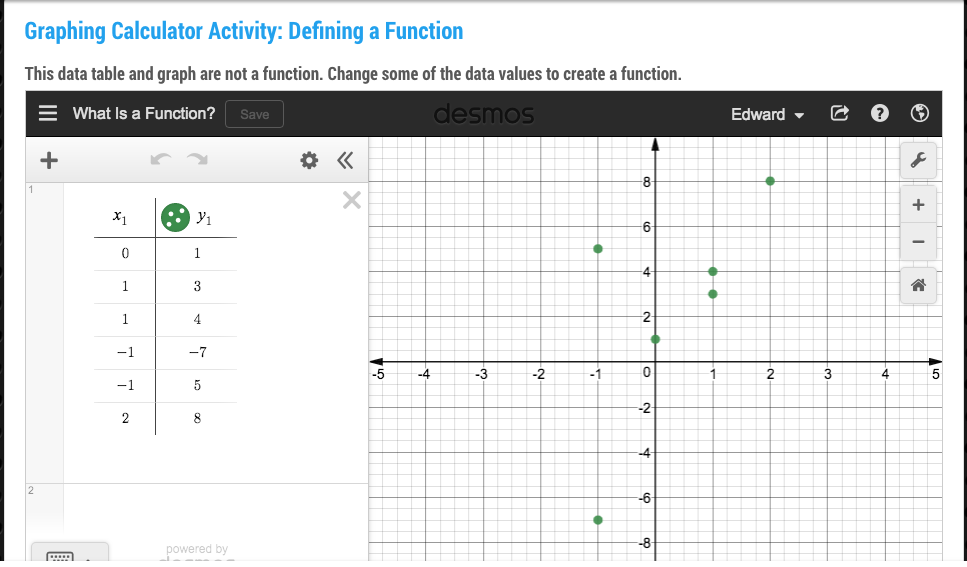
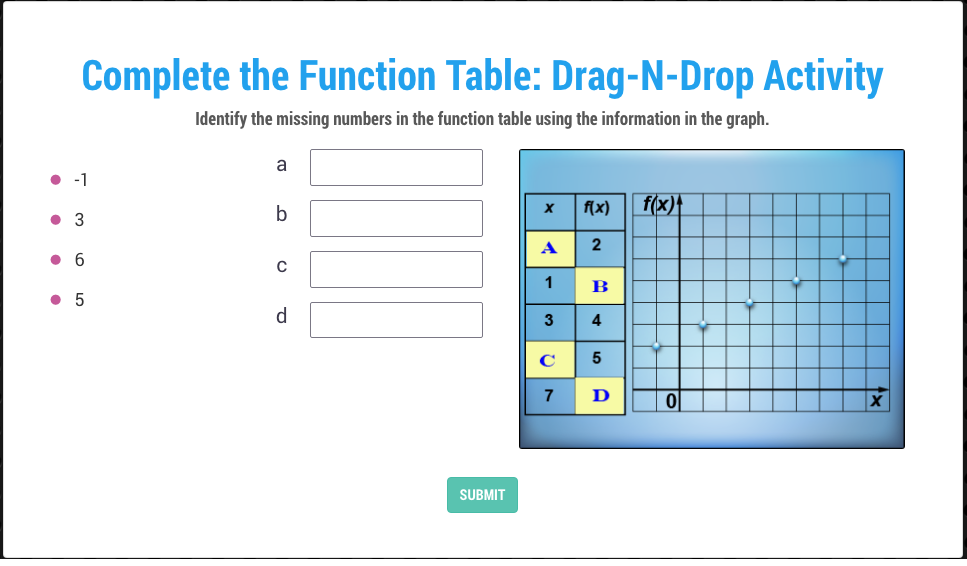
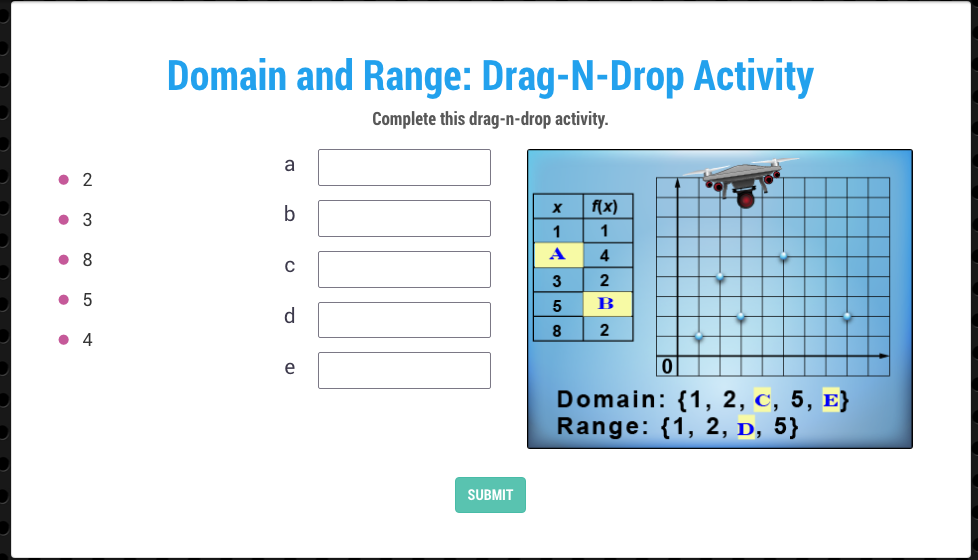
Construction Site Math: Ratios
Description
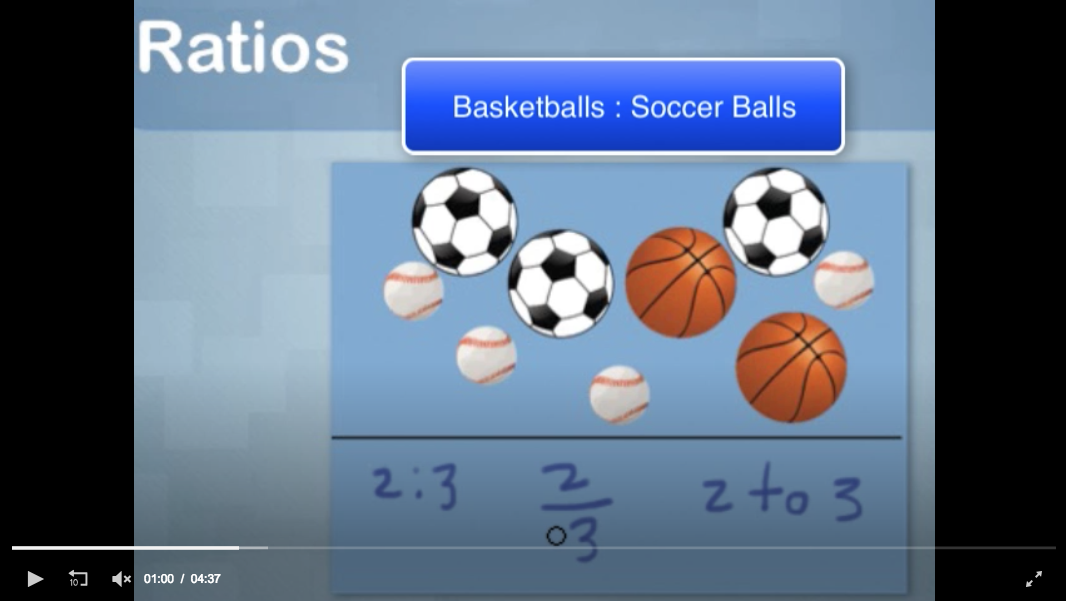
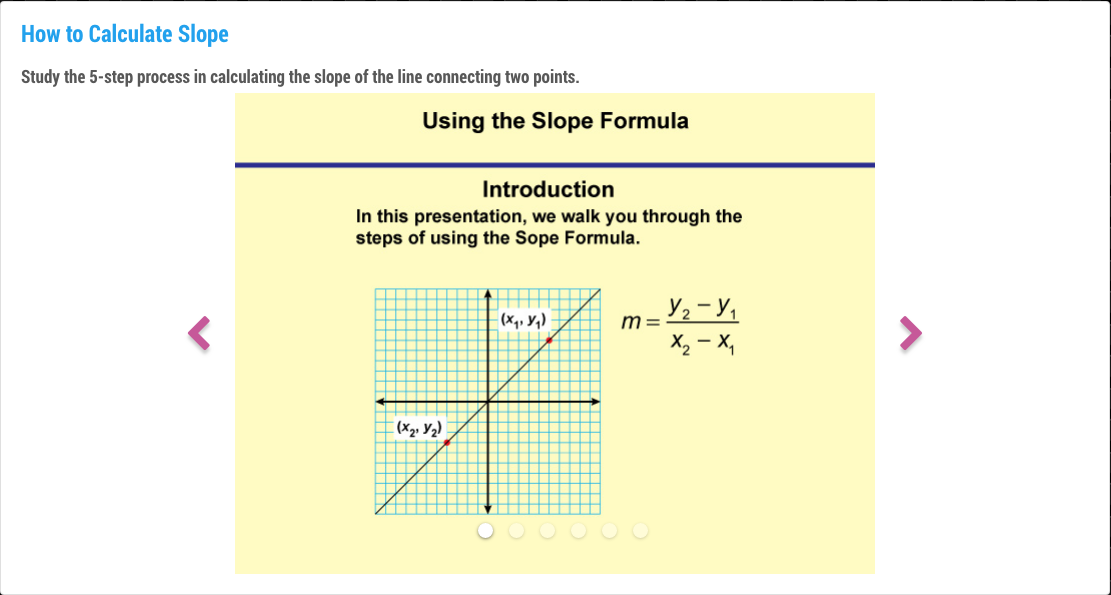
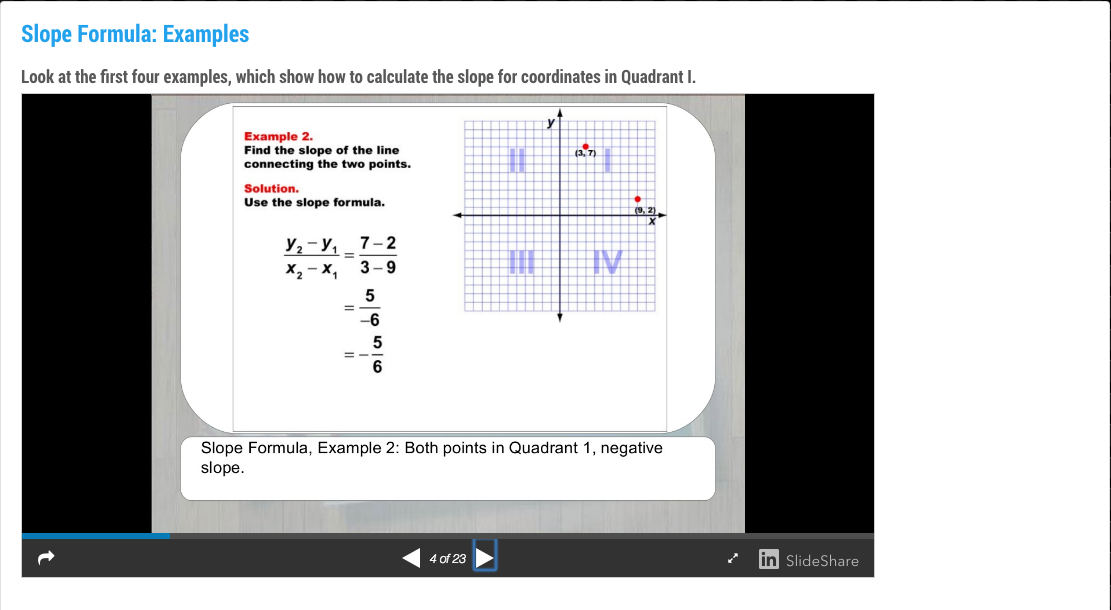
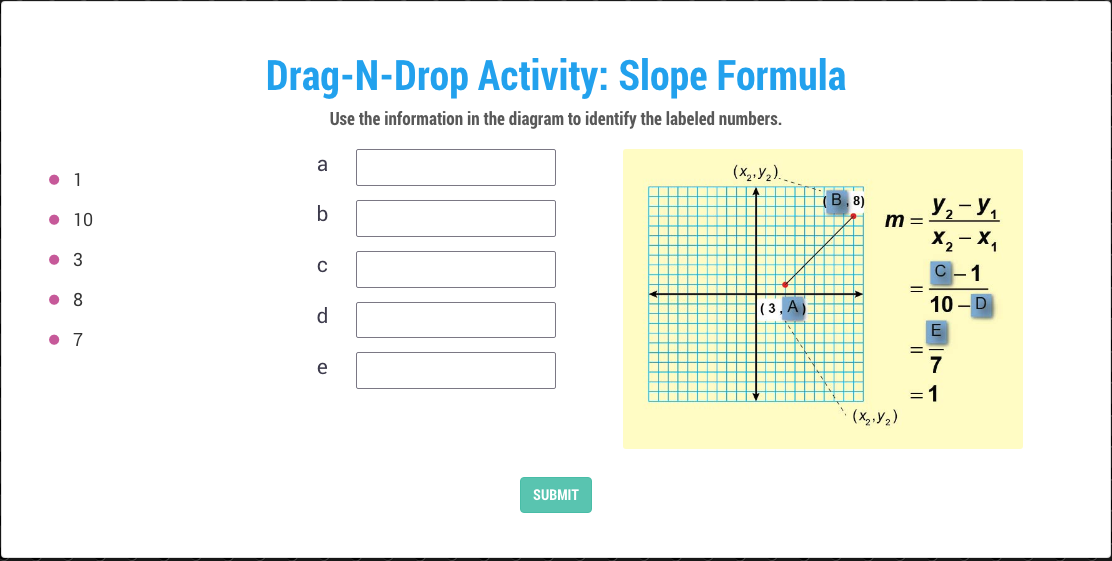
In this real-world application of ratios, students will learn what a ratio is, including ratios with three terms. They will see different ways of writing ratios, including fractions in simplest form.
a:b a to b
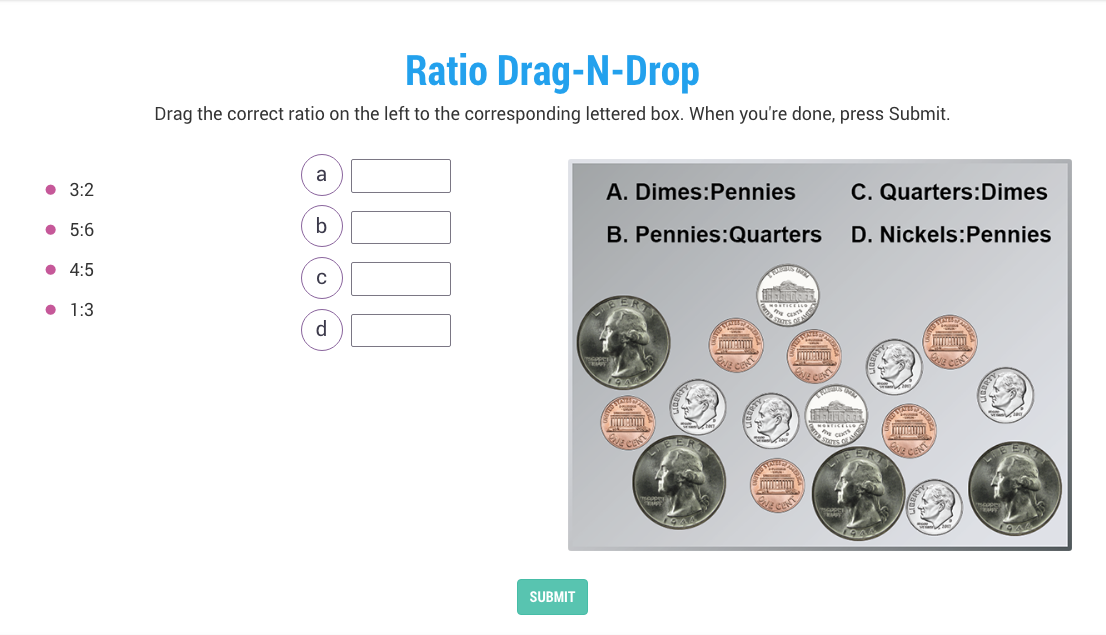
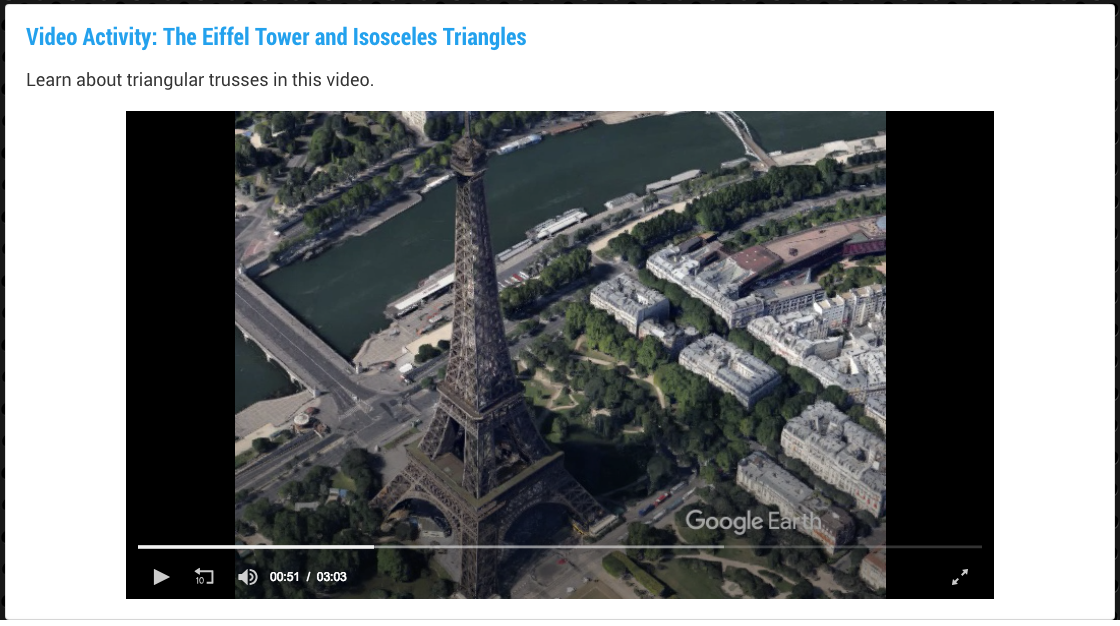
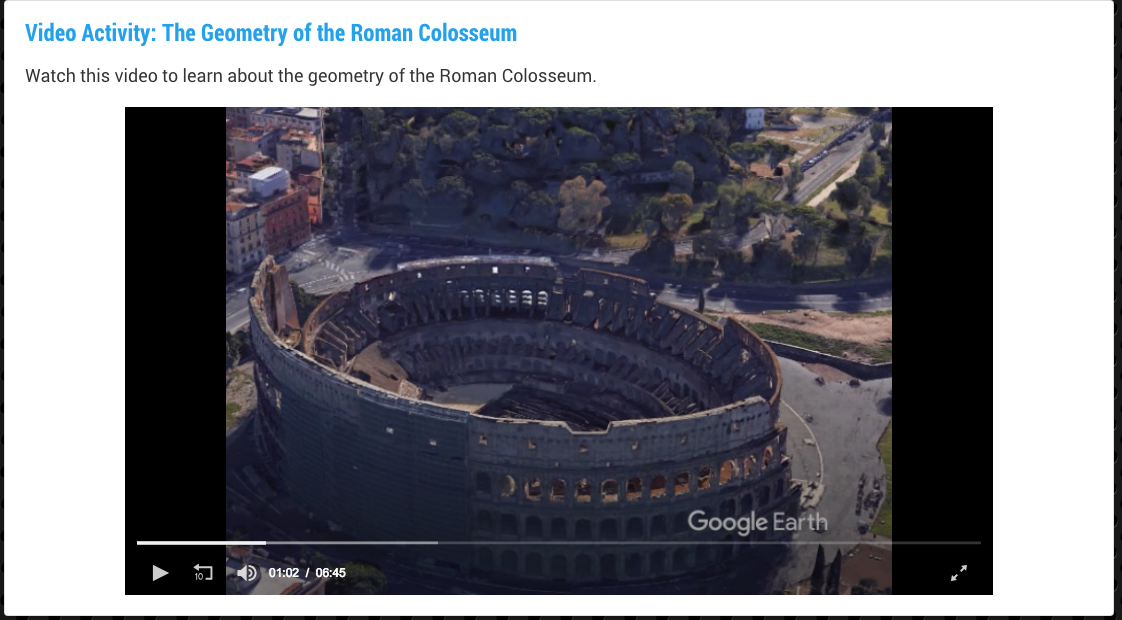
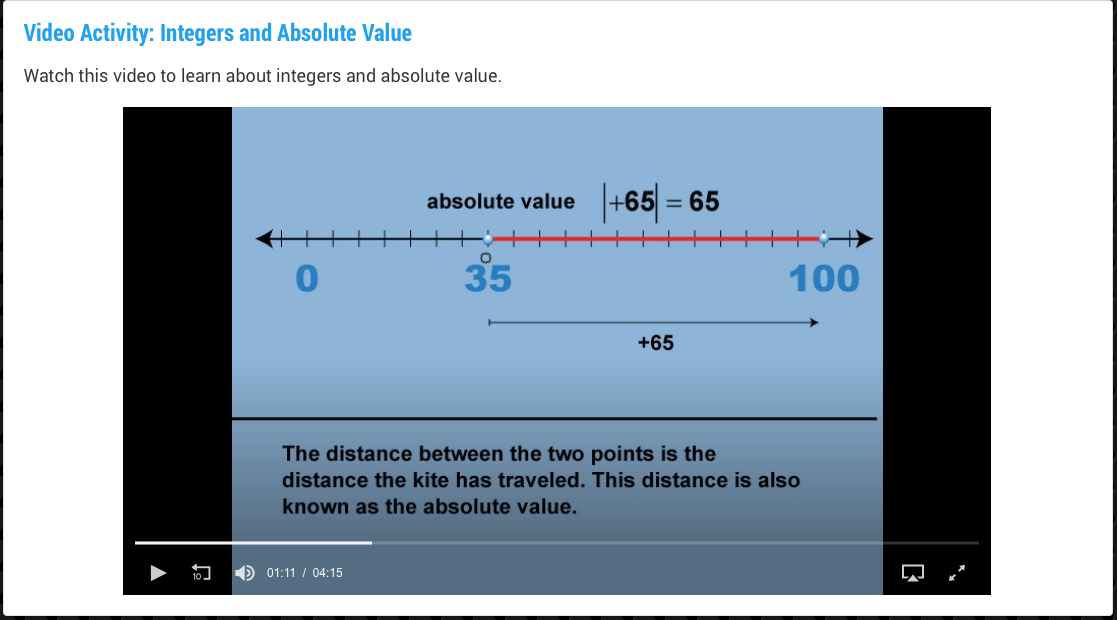
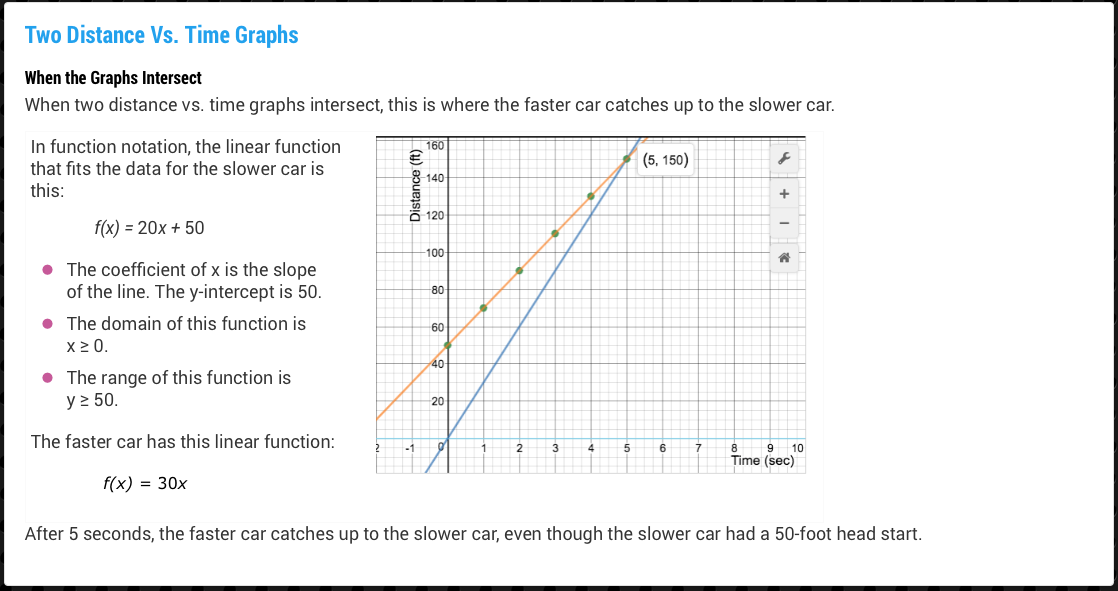
Two short videos introduce the concept of ratios and each video includes real-world examples of ratios. Then several formative assessments are used to test for understanding.
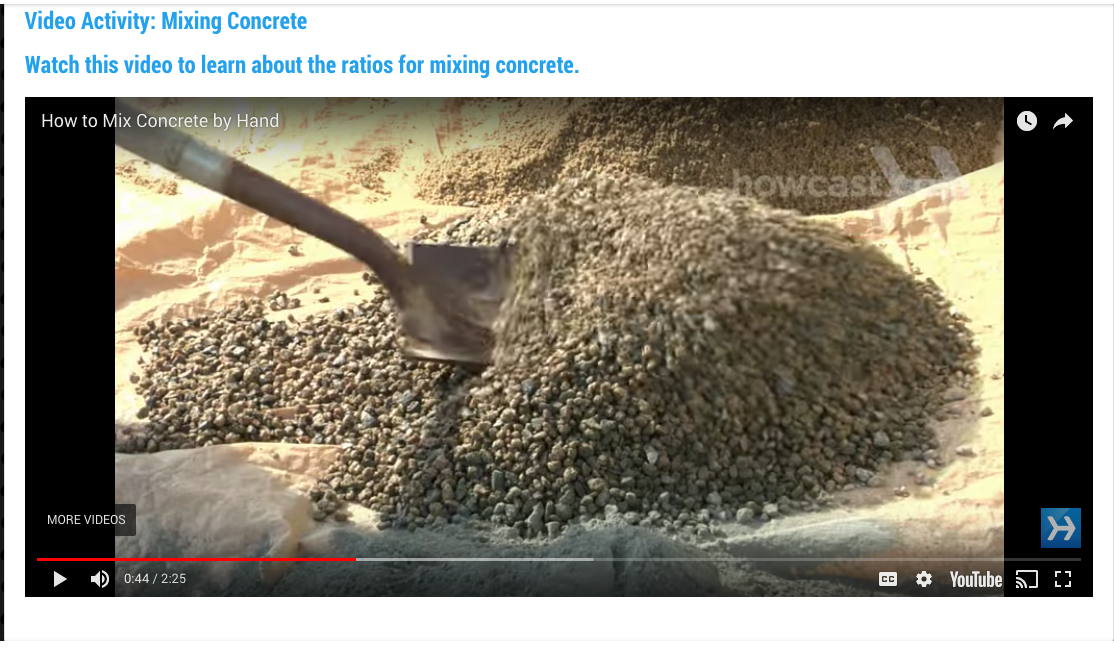
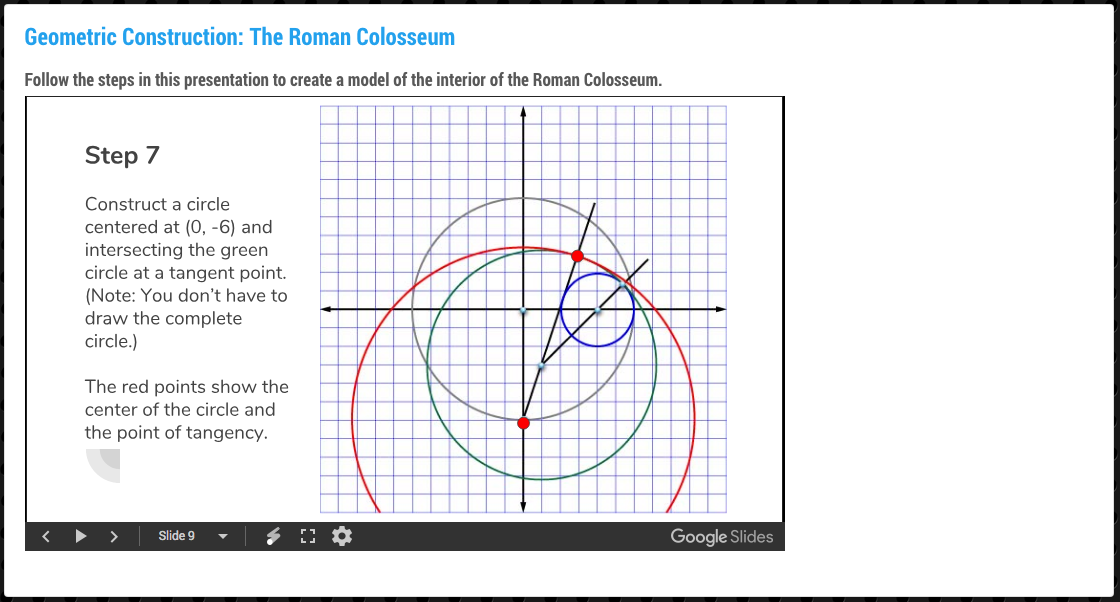
Students then look at the application of ratios to the mixing of concrete at a construction site, starting with a video then followed by an assessment.
This lesson can be assigned to individual students or teams of students. The lesson can be completed in about 20 minutes.
Math Concepts
- Ratios and Rates
- Algebra
Learning Objectives
- Identifying ratios
- Simplifying ratios
- Working with ratios with three items
Prerequisite Skills
- Writing fractions
- Simplifying fractions
| Common Core Standards | CCSS.MATH.CONTENT.6.RP.A.1, CCSS.MATH.CONTENT.7.RP.A.2 |
|---|---|
| Lesson Duration | 20 mins |
| Grade Range | 6th - 7th Grade |