Direct Variation: Circumference vs. Diameter
A simple application of linear functions involves the ratio of the circumference of a circle to its diameter. Students are familiar with the irrational number π, but many may not know where the number comes from.
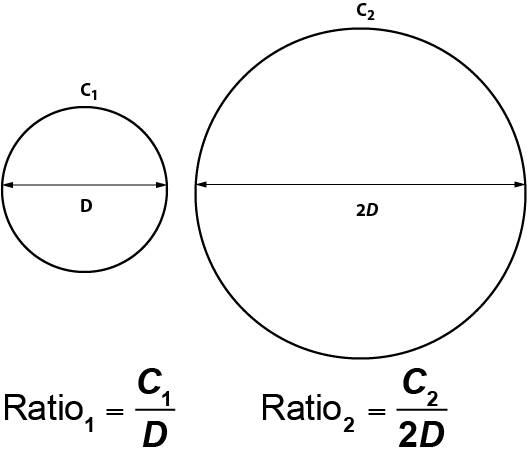
Even students who are familiar with the ratio of circumference to diameter may not realize this represents a linear function. Use function notation to show that circumference (C) is a function of diameter (d).
C = πd
In this form, connect it to the linear function
y = mx
The graph of this equation is a line that crosses the origin. The value of m is the slope, or steepness, of the line.
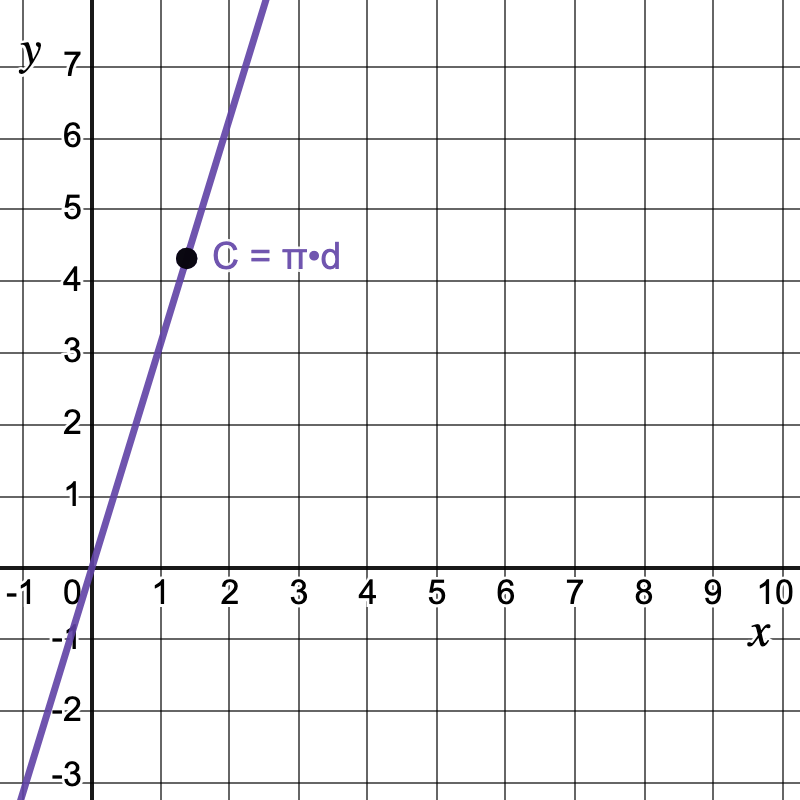
Then write this version of the equation:
y = πx
Ask students what π represents. Have them connect the notion of slope, constant of proportionality, and the ratio of circumference to diameter. The idea that π represents a slope may come as a surprise.
Next, have students calculate the value for π with a hands-on activity. Before doing that review the formula for calculating slope.
m = (y2 - y1)/(x2 - x1)
In the case of direct variation, the graph of the line crosses the origin, whose coordinates are (0, 0). This means that for a direct variation, the slope can be found with one set of coordinates. For example, plug in (0, 0) into the slope formula and you get
m = y/x
Now, to the hands-on activity. Take jar lids of different sizes and string. Have students loop the string around the lid and cut the length of string. Then have them do the same for the diameter.
Have them create a data table of x-y coordinates, where x is the diameter and y is the circumference. Use a spreadsheet to graph the points. The graph will be a scatterplot of a line. If you are using a graphing calculator, find the line of best fit and look at the value for the slope.
For a self-paced student activity on linear functions that focuses on Hooke's Law, take a look at our Classroom Module, linked here: https://www.media4math.com/classroom/browse-modules/applications-linear-functions-circumference-vs-diameter/preview.
Or take a look at our other resources on Hooke's Law: https://www.media4math.com/library/search?keys=circumference+vs+diameter&type=All