Digital Resources on the Topic of Quadratic Equations and Functions

Quadratics

On this page you'll find a sampling of the many resources on Media4Math that focus on the topic of Quadratic Functions. Media4Math is a digital library of over 15,000 resources on all key topics in K-12 math.

Subscribers can download these resources. Register and Subscribe today.

Number of Resources: 873

	Thumbnail Image	Description
Math Worksheet Collection: Completing the Square		This collection aggregates all the math worksheets around the topic of Completing the Square. There are a total of 20 worksheets.
SAT Math Prep—Quadratic Functions and Equations		Description Media4Math Classroom's SAT Math Prep series provide a thorough review of key math topics covered on the SAT. These modules review the key skills that are tested on the SAT with a two-pronged approach:
Math Quiz Collection: The Discriminant		This collection aggregates all the math quizzes on this topic: The Discriminant. There are a total of 60 resources.
Math Video Collection: Anatomy of an Equation		Overview This collectionThis collection aggregates all the math videos and resources in this series: Anatomy of an Equation. There are a total of 105 resources.
Math Video Collection: Texas Instruments Tutorial Videos		Overview This colleThis collection aggregates all the math videos and resources in this series: Texas Instruments Tutorial Videos. There are a total of 266 resources.
Math Video Collection: Video Tutorials Series: Quadratic Equations		This collection aggregates all the math videos and resources in this series: Video Tutorials Series: Quadratic Equations. There are a total of 36 resources.
Math Video Collection: Algebra Applications Video Series: Quadratic Functions		This collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Quadratic Functions. There are a total of 26 resources.
Math Video Collection: Algebra Applications Video Series: Functions and Relations		This collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Functions and Relations. There are a total of 26 resources.
Math Clip Art Collection: Graphs of Functions and Relations		This collection aggregates all the math clip art around the topic of Graphs of Functions and Relations. There are a total of 19 images.
Math Worksheet Collection: Vertex of a Quadratic		This collection aggregates all the math worksheets around the topic of the Vertex of a Quadratic. There are a total of 20 worksheets.
Math Worksheet Collection: Quadratic Functions in Tabular and Graphic Form		This collection aggregates all the math worksheets around the topic of Quadratic Functions in Tabular and Graphic Form. There are a total of 37 worksheets.
Math Worksheet Collection: Properties of Quadratic Functions		This collection aggregates all the math worksheets around the topic of Properties of Quadratic Functions. There are a total of 20 worksheets.
Math Worksheet Collection: Evaluating Quadratic Functions		This collection aggregates all the math worksheets around the topic of Evaluating Quadratic Functions. There are a total of 20 worksheets.
Quizlet Flash Card Collection: Evaluating and Solving Quadratics		This is a collection of Quizlet Flash Cards on the topic of Quadratics. There are 30 Quizlet Flash Card sets.
Math Examples Collection: Solving Simple Quadratic Equations		This collection aggregates all the math examples around the topic of Solving Simple Quadratic Equations. There are a total of 8 Math Examples.
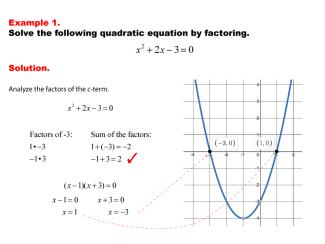
Math Examples Collection: Solving Quadratics by Factoring		This collection aggregates all the math examples around the topic of Solving Quadratics by Factoring. There are a total of 8 Math Examples.
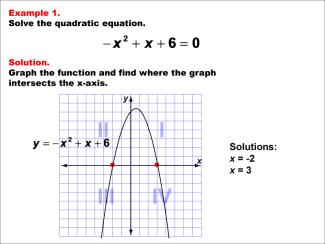
Math Examples Collection: Quadratics with Graphical Solutions		This collection aggregates all the math examples around the topic of Quadratics with Graphical Solutions. There are a total of 8 Math Examples.
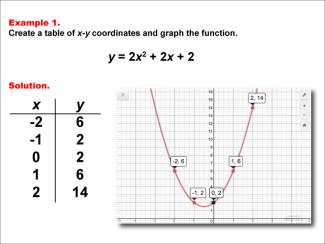
Math Examples Collection: Quadratic Functions in Tabular and Graph Form		This collection aggregates all the math examples around the topic of Quadratic Functions in Tabular and Graph Form. There are a total of 37 Math Examples.
Math Examples Collection: The Quadratic Formula		OThis collection aggregates all the math examples around the topic of the Quadratic Formula. There are a total of 12 Math Examples.
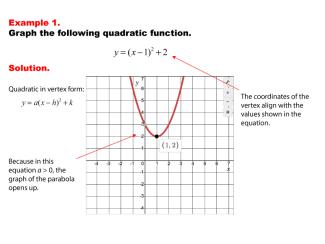
Math Examples Collection: Graphs of Quadratic Functions in Vertex Form		This collection aggregates all the math examples around the topic of Graphs of Quadratic Functions in Vertex Form. There are a total of 8 Math Examples.
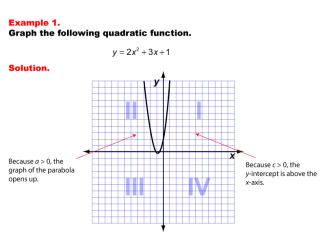
Math Examples Collection: Graphs of Quadratic Functions in Standard Form		This collection aggregates all the math examples around the topic of Graphs of Quadratic Functions in Standard Form. There are a total of 18 Math Examples.
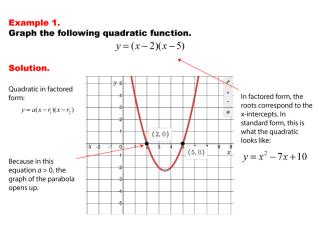
Math Examples Collection: Graphs of Quadratic Functions in Factored Form		This collection aggregates all the math examples around the topic of Graphs of Quadratic Functions in Factored Form. There are a total of 8 Math Examples.
Math Examples Collection: Factoring Quadratics		This collection aggregates all the math examples around the topic of Factoring Quadratics. There are a total of 11 Math Examples.
Math Examples Collection: The Discriminant		OverviewThis collection aggregates all the math examples around the topic of Calculating the Discriminant. There are a total of 10 Math Examples.
Math Examples Collection: Difference of Squares and Cubes		This collection aggregates all the math examples around the topic of the Difference of Squares and Cubes. There are a total of 11 Math Examples.