Display Title
Definition--Quadratics Concepts--Complex Roots
Display Title
Complex Roots

Topic
Quadratics Concepts
Definition
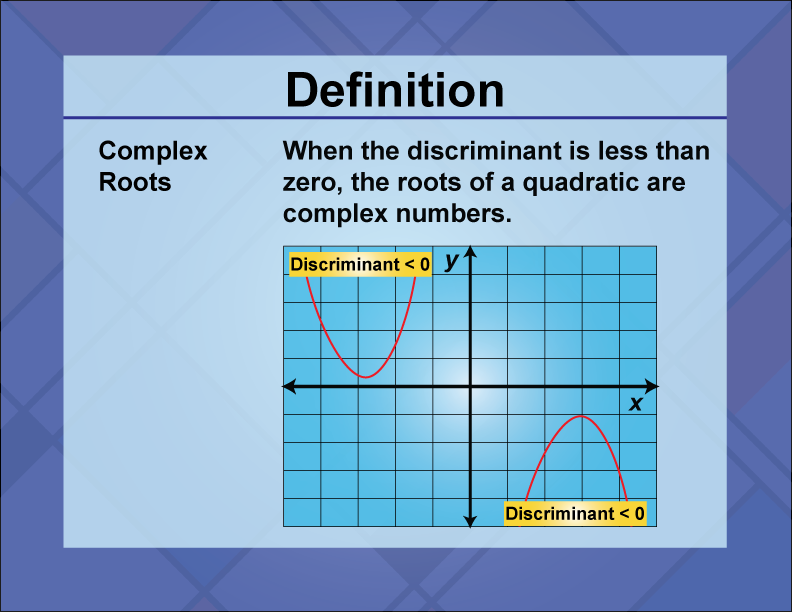
Complex roots are solutions to a quadratic equation that are not real numbers, often involving the imaginary number i.
Description
Complex roots occur when the discriminant of a quadratic equation
ax2 + bx + c = 0
is negative, indicating that the parabola does not intersect the x-axis. These roots are expressed in the form
a ± bi
where a and b are real numbers, and i is the imaginary unit. Complex roots are essential in fields such as engineering and physics, where they are used to model oscillations, waves, and other phenomena that involve complex numbers. In math education, understanding complex roots is crucial for solving quadratic equations with no real solutions and for exploring the broader concept of complex numbers. This knowledge helps students appreciate the completeness of the number system and the various types of solutions that quadratic equations can have. An example of complex roots can be seen in the equation
x2 + 4 = 0
which has roots x = ±2i.
For a complete collection of terms related to Quadratic Expressions, Functions, and Equations click on this link: Quadratics Collection
| Common Core Standards | CCSS.MATH.CONTENT.HSN.CN.C.7, CCSS.MATH.CONTENT.HSA.SSE.B.3.B, CCSS.MATH.CONTENT.HSA.REI.B.4.A, CCSS.MATH.CONTENT.HSF.IF.C.8.A |
|---|---|
| Grade Range | 6 - 10 |
| Curriculum Nodes |
Algebra • Quadratic Functions and Equations • Quadratic Equations and Functions |
| Copyright Year | 2021 |
| Keywords | quadratic functions, quadratic equations, quadratic formula, definitions, glossary terms |