Display Title
Definition | 3D Geometry Concepts | Net for a Dodecahedron
Display Title
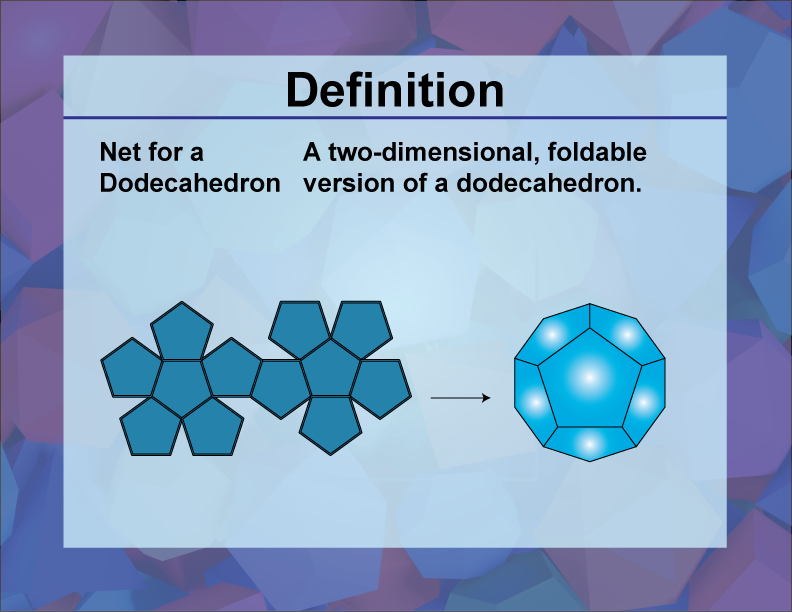
Net for a Dodecahedron

Topic
3D Geometry.
Definition
A net for a dodecahedron is a two-dimensional figure that can be folded to form a three-dimensional dodecahedron.
Description
The dodecahedron is one of the five Platonic solids, characterized by its twelve regular pentagonal faces, thirty edges, and twenty vertices. Understanding the net of a dodecahedron helps in visualizing and constructing this complex polyhedron from a flat sheet.
In three-dimensional geometry, nets are essential for comprehending the structure and properties of polyhedra. By studying the net of a dodecahedron, students and researchers can gain insights into the spatial relationships between its faces and vertices. This understanding is not only fundamental in pure mathematics but also has practical applications in fields such as architecture, engineering, and computer graphics, where three-dimensional modeling is essential.
The net for a dodecahedron also aids in exploring symmetry and topology within geometric figures. It provides a hands-on approach to learning, allowing for the physical manipulation of shapes to better grasp theoretical concepts. In educational settings, constructing a dodecahedron from its net can enhance spatial reasoning skills and foster a deeper appreciation for geometric principles.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • 3-Dimensional Figures |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |