
These are the resources that support this NYS Standard.
NY-AI-A.SSE.1a: Write the standard form of a given polynomial and identify the terms, coefficients, degree, leading coefficient, and constant term.
There are 183 resources.| Title | Description | Thumbnail Image | Curriculum Topics |
|---|---|---|---|
Math Definitions Collection: Linear Functions |
This collection aggregates all the definition image cards around the topic of Linear Functions vocabulary. There are a total of 19 terms. | 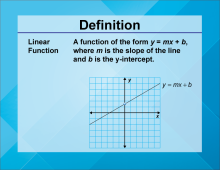
|
Slope-Intercept Form, Applications of Linear Functions, Graphs of Linear Functions, Standard Form, Point-Slope Form and Slope |
Math Video Definitions Collection: Linear Expressions, Functions, and Equations |
This collection aggregates all the video definitions around the topic of Linear Expressions, Functions, and Equations terms and vocabulary. There are a total of 34 videos. This collection of resources is made up of downloadable MP4 files that you can easily incorporate into a presentation. | 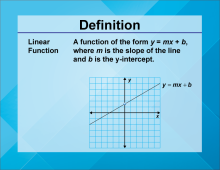
|
Slope-Intercept Form, Applications of Linear Functions, Graphs of Linear Functions, Point-Slope Form, Slope, Standard Form, Solving Systems of Equations, Proportions, Data Analysis, Variable Expressions, Functions and Their Inverses, Special Functions, Polynomial Expressions and Numerical Expressions |
Math Worksheet Collection: Analyzing Expressions |
This collection aggregates all the math worksheets around the topic of Analyzing Expressions. There are a total of 5 worksheets. | 
|
Numerical and Algebraic Expressions |
Math Video Collection: Anatomy of an Equation |
Overview This collectionThis collection aggregates all the math videos and resources in this series: Anatomy of an Equation. There are a total of 105 resources. | 
|
Solving One-Step Equations, Solving Two-Step Equations, Quadratic Equations and Functions and Standard Form |
Desmos Worksheets and Transcripts |
OverviewThis is a collection of companion resources, including worksheets and transcripts. The worksheets accompany some of the Desmos graphing calculator activities. The transcripts are for the videos. | 
|
Slope-Intercept Form, Quadratic Equations and Functions, Standard Form, Point-Slope Form, Definition of an Angle, Definition of a Line, Parallel Lines, Perpendicular Lines, Definition of a Plane, Definition of a Triangle, Geometric Constructions with Triangles, Definition of a Quadrilateral, Geometric Constructions with Polygons and Definition of a Polygon |
Interactive Media Collection: Point-Slope Form |
This collection aggregates all the math videos and other resources on the topic of the Point-Slope Form. There are seven resources. | 
|
Point-Slope Form, Slope-Intercept Form, Calculus Vocabulary, Applications of Linear Functions and Graphs of Linear Functions |
Interactive Media Collection: Linear Equations in Standards Form |
This collection aggregates all the math videos and other resources on the topic of Linear Equations in Standard Form. here are seven resources. | 
|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 1: Ax + By = C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 1: Ax + By = C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: Ax + By = C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 2: Ax + By = -C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 2: Ax + By = -C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: Ax + By = -C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 3: Ax - By = C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 3: Ax - By = C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: AX - By = C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 4: -Ax + By = C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 4: -Ax + By = C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: -Ax + By = C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 5: Ax - By = -C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 5: Ax - By = -C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: AX - By = -C. . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 6: -Ax + By = -C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 6: -Ax + By = -C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: -AX + By = -C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 7: -Ax - By = C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 7: -Ax - By = C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: -AX - By = C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 8:-Ax - By = -C |
Closed Captioned Video: Anatomy of an Equation: Linear Equations in Standard Form to Slope-Intercept Form 8:-Ax - By = -C
In this video tutorial, analyze the steps in converting a linear equation in Standard Form to a linear function in Slope-Intercept Form. In this video we work with this version of the Standard Form: -AX - By = -C. . . |

|
Standard Form |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 1 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 1
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: ax^2 + bx + c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 2 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 2
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: ax^2 + bx - c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 3 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 3
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: ax^2 - bx + c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 4 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 4
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: -ax^2 + bx + c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 5 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 5
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: ax^2 - bx - c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 6 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 6
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: -ax^2 + bx - c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 7 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 7
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: -ax^2 - bx + c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 8 |
Closed Captioned Video: Anatomy of an Equation: Quadratic Equations 8
In this video, analyze the steps in solving a quadratic equation with two roots. In this video we work with this version of the quadratic equation: -ax^2 - bx - c = 0. . . |

|
Quadratic Equations and Functions |
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 1 |
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 1
In this video learn the mechanics of solving a two-step equation involving addition and multiplication. . |

|
Solving Two-Step Equations |
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 10 |
Closed Captioned Video: Anatomy of an Equation: Two-Step Equations 10
In this video learn the mechanics of solving a two-step equation involving addition and division. In this variation, the x-term has a negative coefficient. . |

|
Solving Two-Step Equations |

