
These are the resources that support this Florida Standard.
MAFS.6.NS.2.4: Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1–100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 (9 + 2).
There are 104 resources.| Title | Description | Thumbnail Image | Curriculum Topics |
|---|---|---|---|
Math Video Definitions Collection: Fractions |

|
Compare and Order Fractions and Fractions and Mixed Numbers | |
Math Definitions Collection: Fractions |

|
Compare and Order Fractions, Fractions and Mixed Numbers and Identify and Name Fractions | |
Math Definitions Collection: Factors and Multiples |

|
Numerical Expressions | |
Math Video Collection: Video Tutorials Series: The Distributive Property |

|
Numerical and Algebraic Expressions | |
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negative |
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negativeVideo Tutorial: The Distributive Property: a(-x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x + b), a negative, b negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positive |
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positiveVideo Tutorial: The Distributive Property: a(-x + b), a negative, b positive. In this video use the distributive property with an expression of the form a(-x + b), a negative, b positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(-x + b), all constants positive |
Closed Captioned Video: The Distributive Property: a(-x + b), all constants positiveVideo Tutorial: The Distributive Property: a(-x + b), all constants positive. In this video use the distributive property with an expression of the form a(-x + b), all constants positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negative |
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negativeVideo Tutorial: The Distributive Property: a(-x - b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x - b), a negative, b negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positive |
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positiveVideo Tutorial: The Distributive Property: a(-x - b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(-x - b), a negative, b positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(-x - b), all constants positive |
Closed Captioned Video: The Distributive Property: a(-x - b), all constants positiveVideo Tutorial: The Distributive Property: a(-x - b), all constants positive. In this video use the distributive property with an expression of the form a(-x - b), all constants positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positive |
Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positiveVideo Tutorial: The Distributive Property: a(bx + c), a negative, b and c positive. In this video, we will use the distributive property with an expression of the form a(bx + c), a negative, b and c positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx + c), all constants negative |
Closed Captioned Video: The Distributive Property: a(bx + c), all constants negativeVideo Tutorial: The Distributive Property: a(bx + c), all constants negative. In this video use the distributive property with an expression of the form a(bx + c), all negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx + c), all constants positive |
Closed Captioned Video: The Distributive Property: a(bx + c), all constants positiveVideo Tutorial: The Distributive Property: a(bx + c), all constants positive. In this video use the distributive property with an expression of the form a(bx + c), all constants positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positive |
Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positiveVideo Tutorial: The Distributive Property: a(bx - c), a negative, b and c positive. In this video use the distributive property with an expression of the form a(bx - c), a negative, b and c positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx - c), all constants negative |
Closed Captioned Video: The Distributive Property: a(bx - c), all constants negativeVideo Tutorial: The Distributive Property: a(bx - c), all constants negative. In this video, we will use the distributive property with an expression of the form a(bx - c), all negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(bx - c), all constants positive |
Closed Captioned Video: The Distributive Property: a(bx - c), all constants positiveVideo Tutorial: The Distributive Property: a(bx - c), all constants positive. In this video use the distributive property with an expression of the form a(bx - c), all constants positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negative |
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negativeVideo Tutorial: The Distributive Property: a(x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(x + b), a negative, b negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positive |
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positiveVideo Tutorial: The Distributive Property: a(x + b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(x + b), a negative, b positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x + b), all constants positive |
Closed Captioned Video: The Distributive Property: a(x + b), all constants positiveVideo Tutorial: The Distributive Property: a(x + b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x + b), all constants positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negative |
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negativeVideo Tutorial: The Distributive Property: a(x - b), a negative, b negative. In this video, we will use the distributive property with an expression of the form a(x - b), a negative, b negative. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positive |
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positiveVideo Tutorial: The Distributive Property: a(x - b), a negative, b positive. In this video use the distributive property with an expression of the form a(x - b), a negative, b positive. |

|
Numerical and Algebraic Expressions |
Closed Captioned Video: The Distributive Property: a(x - b), all constants positive |
Closed Captioned Video: The Distributive Property: a(x - b), all constants positiveVideo Tutorial: The Distributive Property: a(x - b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x - b), all constants positive. |

|
Numerical and Algebraic Expressions |
Definition--Common Factor |
Definition--Common FactorThis is part of a collection of math definitions from Media4Math's Visual Glossary. |

|
Numerical Expressions and Variable Expressions |
Definition--Factors and Multiples--Area Models for Factors |
Definition--Factors and Multiples--Area Models for FactorsThis is a collection of definitions related to factors and multiples. This includes general definitions for factors and multiples, as well as related terms around common factors and multiples, LCM, LCD, visual models, and applications of these concepts in other areas of math. |
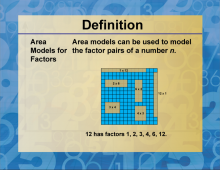
|
Numerical Expressions |
Definition--Factors and Multiples--Common Factors |
Definition--Factors and Multiples--Common FactorsThis is a collection of definitions related to factors and multiples. This includes general definitions for factors and multiples, as well as related terms around common factors and multiples, LCM, LCD, visual models, and applications of these concepts in other areas of math. |

|
Numerical Expressions |

