Display Title
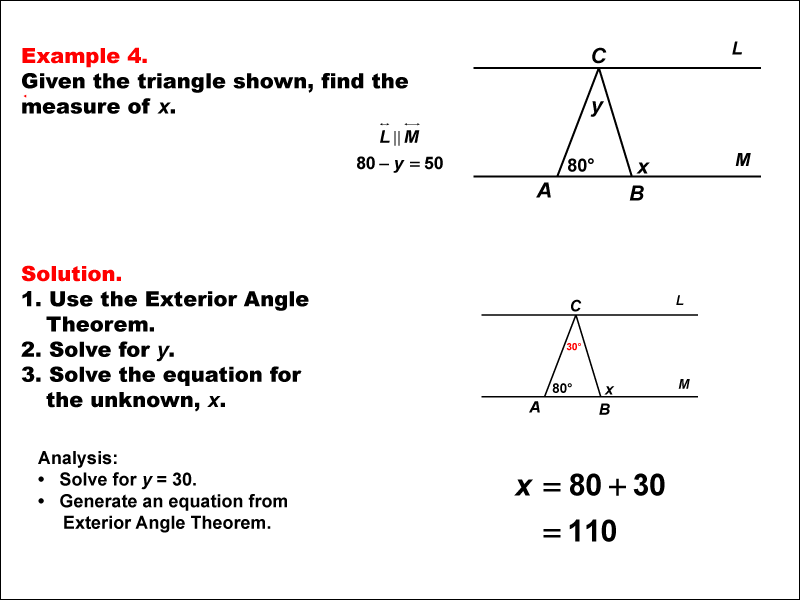
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4
Display Title
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4
This is part of a collection of math examples that focus on solving different types of equations.
To see the complete library of math examples, click on this link.
Note: The download is an image file.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.CO.C.10, CCSS.MATH.CONTENT.HSA.CED.A.1 |
|---|---|
| Grade Range | 9 - 11 |
| Curriculum Nodes |
Algebra • Expressions, Equations, and Inequalities • Applications of Equations and Inequalities Geometry • Triangles • Applications of Triangles |
| Copyright Year | 2022 |
| Keywords | triangles, solving equations |