Display Title
Math Clip Art: Parallel Lines Cut by a Transversal 2
Display Title
Math Clip Art: Parallel Lines Cut by a Transversal 2
This collection of clip art images show the various angles formed by two parallel lines cut by a transversal. This includes alternate interior angles, alternate exterior angles, corresponding angles, vertical angles, supplementary angles, same side interior angles, and same side exterior angles. All transversal lines and angles are clearly marked and can be used in a presentation on the properties of parallel lines cut by a transversal.
—PRESS PREVIEW TO SEE THE CLIP ART IMAGE—
To see the complete collection of these clip art images, click on this link.
The next section provides background information on parallel lines cut by a transversal.
Parallel Lines Cut by a Transversal
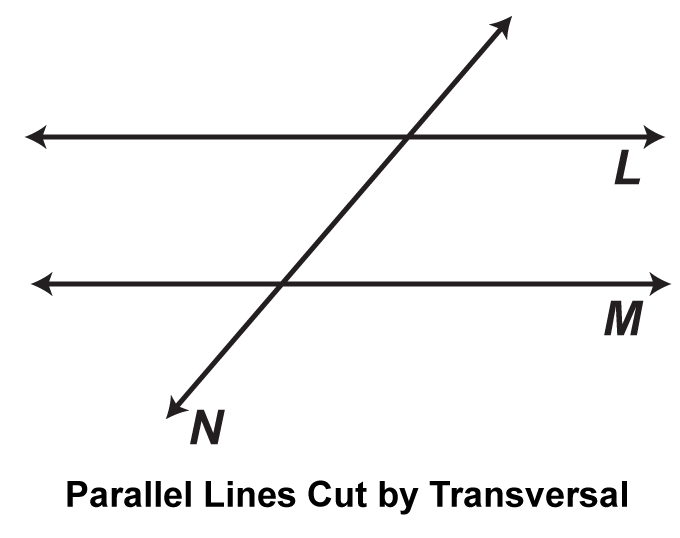
Parallel lines are on the same plane and do not intersect. Here are two lines, L and M, that are on plane P and parallel.
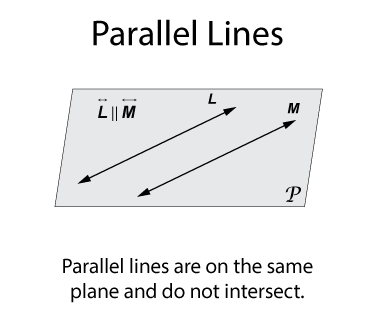
Parallel lines are are always the same distance from each other. In this illustration the dashed segment indicates the distance between the two lines. That distance doesn't change.
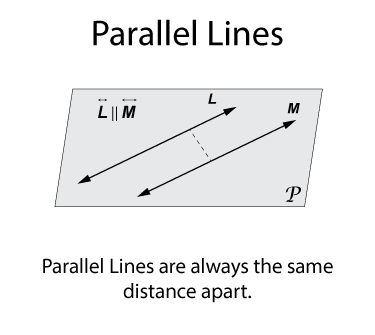
A line that intersects the parallel lines is called a transversal. In the illustration below you can see transveral N that insersects lines L and M.
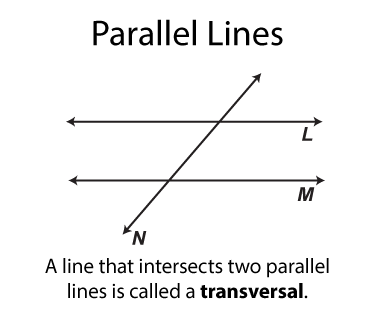
When parallel lines are cut by a transversal, there are number of set of angles whose properties are important to remember. The categories of angles include:
- Alternate interior angles
- Alternate exterior angles
- Same side interior angles
- Same side exterior angles
- Supplementary angles
- Vertical angles
Let's start with the alternate interior angles, which are shown here. There are two sets of alternate interior angles. These pairs of angles are congruent. The word "alternate" means "opposite" In each case the one angle is on the opposite side of the transversal from the other angle.
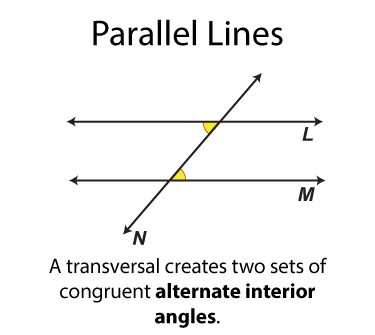
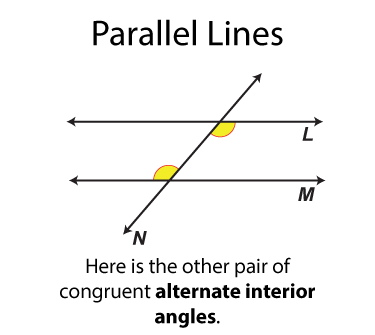
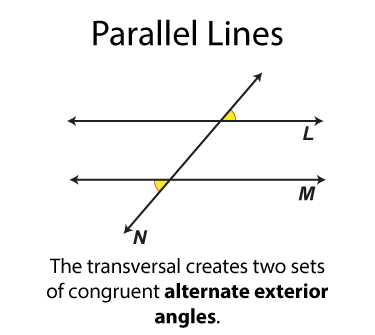
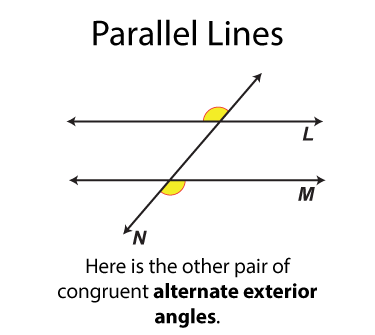
The next set of angles are called alternate exterior angles. There are two sets. Each set of angles is congruent. Each angle is on one side of the transversal from the other angle it is congruent to.
The next set of angles are called corresponding angles. There are four sets. Each set of angles is congruent. Each set of angles is on the same side of the transversal.
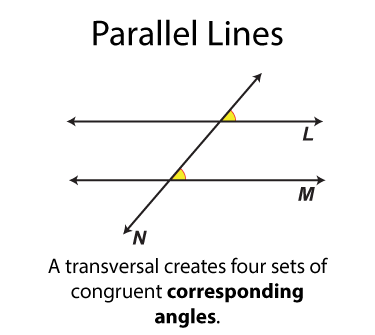
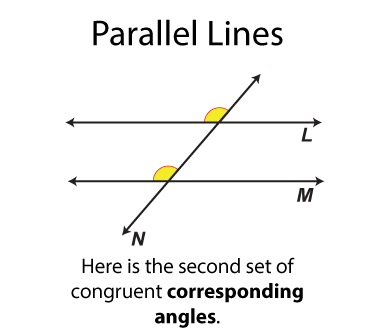
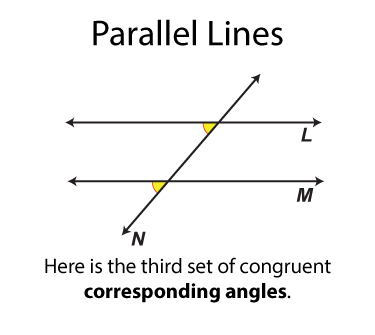
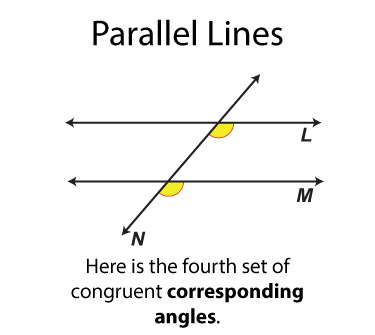
The next set of angles are called vertical angles. There are two sets. Each set of angles is congruent. (By definition all vertical angles are congruent.) Each angle is on on the opposite side of the transversal from the other angle it is congruent to.
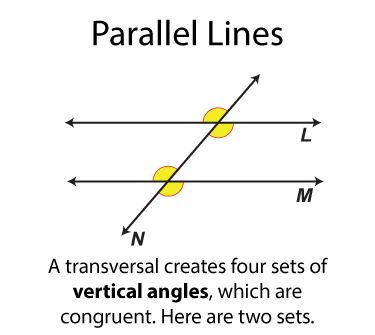
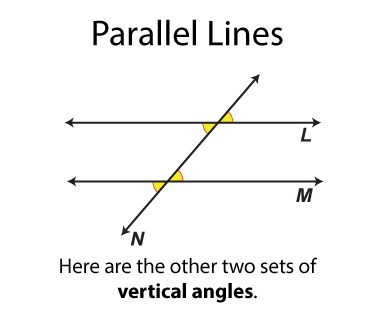
The next set of angles are called vertical angles. There are two sets. Each set of angles is congruent. (By definition all vertical angles are congruent.) Each angle is on on the opposite side of the transversal from the other angle it is congruent to.


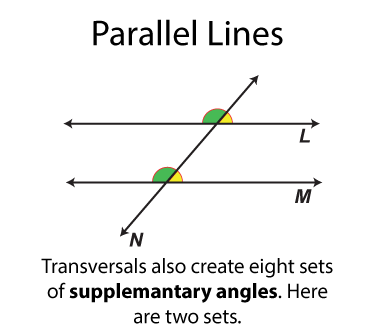
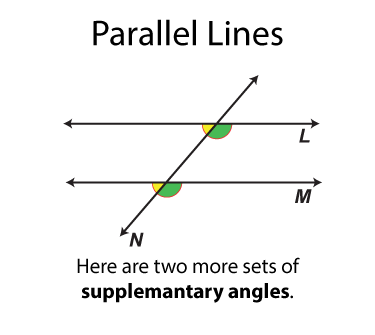
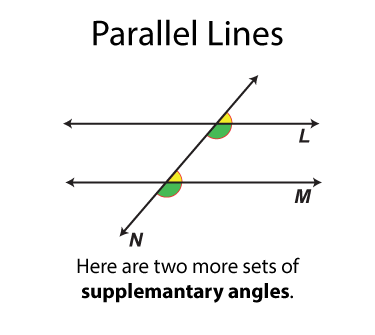
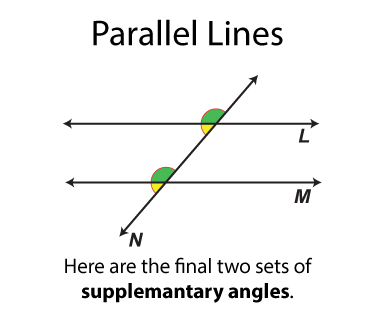
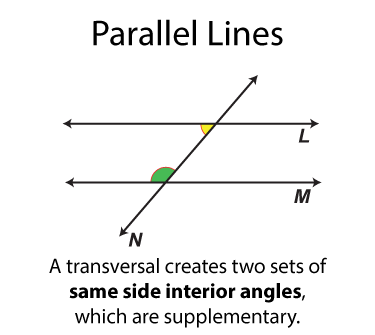
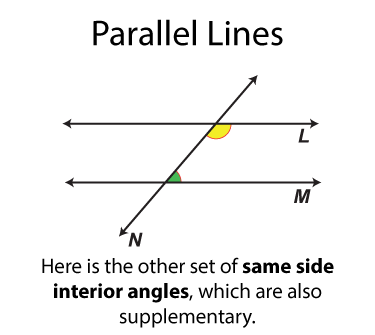
The next set of angles are supplementary angles. There are eight sets. By definition the supplementary angles add up to 180°. Some pairs of supplementary angles are on opposite sides of the transversal and some are on the same side.
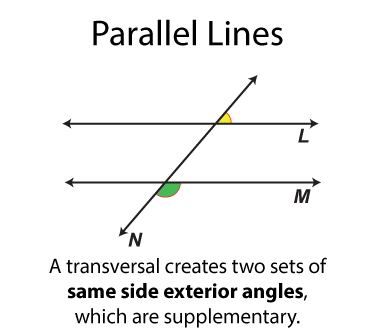
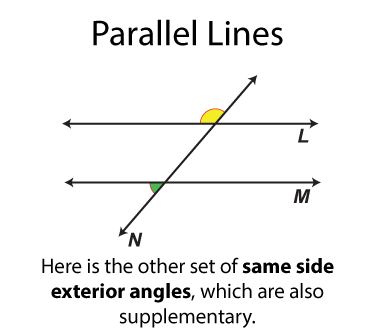
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math clip art on this topic. To see the complete clip art collection, click on this link.
To learn more about Slide Show Creator, click on this Link:
Accessibility
This resource can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.CONTENT.4.G.A.2, CCSS.MATH.CONTENT.8.G.A.5 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Points and Lines • Parallel Lines |
| Copyright Year | 2014 |
| Keywords | Parallel Lines Cut by a Transversal, parallel lines, transversal, vertical angles, supplementary angles, alternate interior angles, alternate exterior angles |