
Display Title
Definition--Integer
Display Title
Integers
This is part of a collection of images that cover key vocabulary on a variety of math topics.
—PRESS PREVIEW TO SEE THE IMAGE—
To see the complete collection of definitions, click on this link.
The following section includes background information on integers (and also rational numbers). Refer to this section as you view the videos, or as review material afterward.
Video Tutorial: Integers

The video was uploaded on 9/13/2022.
You can view the video here.
The video lasts for 4 minutes and 56 seconds.
What Are Integers?
In arithmetic you learned that whole numbers include zero and the counting numbers from 1 to infinity.
Whole numbers don’t include:
- Fractional values
- Decimal values
Integers include the whole numbers, zero, and positive numbers 1, 2, 3, etc., but also includes a different class of numbers, negative numbers.
Representing Integers
You can use a number line to represent the integers.
Notice that every integer and its opposite is the same distance from 0 on the number line. Also, the arrow heads on the number line mean that the integers extend to infinity.
Representing distance on a number line is shown below.

Distance is always a positive number, so use the absolute value symbol to ensure the result is positive. Subtract one value from another and find the absolute value of the difference.
Every integer has its opposite. Notice on the number line that 1 and -1 are opposites, as are 2 and -2, and so on. Every integer and its opposite is the same distance from zero on the number line, as shown below.
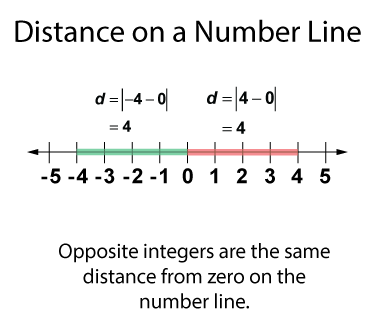
As you can see both 4 and -4 are four units from zero. This same pattern applies to all integers and their opposites. Also, the sum of any integer and its opposite is zero.
1 + (-1) = 0
2 + (-2) = 0
This pattern continues for all integers and their opposites.
The technique of finding the absolute value of a difference applies to any pair of integers, as shown below.

Integers can also be represented using algebra tiles, as shown below.

Comparing and Ordering Integers
You can use a number line to compare and order numbers. In going from left to right on the number line, numbers increase in value. In going from right to left on the number line, numbers decrease in value. See the example below.

Knowing this property of integers on a number line, suppose there are four integers that satisfy these inequalities:
C < D < B < A
We can graph these integers on a number line as shown below.

Adding and Subtracting Integers
When adding and subtracting integers, you need to keep track of the sign of each number. There are several examples to consider.
Example 1: Adding Two Positive Integers
1 + 2 + 3
This is similar to adding whole numbers. The result is positive.
Example 2: Adding Two Negative Integers
-2 + (-3) = -5
Adding two negative integers results in a negative integer.
Example 3: Adding a Positive Integer and a Negative Integer
5 + (-2) = 5 - 2 = 3
Adding integers with opposite signs can be rewritten as whole number subtraction. The result can be positive, negative, or zero.
Example 4: Subtracting Two Positive Integers
2 - 5 = -3
This is somewhat similar to whole number subtraction. The result can be positive, negative or zero.
Example 5: Subtracting Two Negative Integers
-5 - (-7) = -5 + 7 = 2
When subtracting by a negative, the negative number changes to a positive number. The result can be positive, negative, or zero.
Example 1: Subtracting Positive and Negative Integers
-7 - 2 = -9
When subtracting a positive, treat it the same as adding a negative. When subtracting a negative, the operation changes to addition.
Multiplying Integers
When multiplying integers, you need to keep track of the sign of each number. There are several cases to consider.
Case 1: Multiplying Two Positive Integers
2 • 4 = 8
This is similar to multiplying whole numbers. The result is positive.
Case 2: Multiplying a Positive Integer and a Negative Integer
-2 • 4 = -8
This is somewhat similar to multiplying whole numbers. The result is negative.
Case 3: Multiplying Two Negative Integers
-2 • (-4) = 8
When multiplying two negatives, the product is positive.
Dividing Integers
By definition a rational number is the ratio of two integers. This is the same as dividing by two integers. Integer division is the definition of a rational number. Consider two integers a and b. A rational number is defined as follows:
a ÷ b
With both rational numbers and integer division, b cannot equal zero. The rules for integer division, in terms of the sign of the quotient, are similar to those for multiplication.
Note: The download is a PNG file.
Related Resources
To see additional resources on this topic, click on the Related Resources tab.
Create a Slide Show
Subscribers can use Slide Show Creator to create a slide show from the complete collection of math definitions on this topic. To see the complete collection of definitions, click on this Link.
To learn more about Slide Show Creator, click on this Link.
Accessibility
This resources can also be used with a screen reader. Follow these steps.
-
Click on the Accessibility icon on the upper-right part of the screen.

-
From the menu, click on the Screen Reader button. Then close the Accessibility menu.

-
Click on the PREVIEW button on the left and then click on the definition card. The Screen Reader will read the definition.
| Common Core Standards | CCSS.MATH.PRACTICE.MP5 |
|---|---|
| Grade Range | 6 - 12 |
| Curriculum Nodes |
Algebra • The Language of Math • Numerical Expressions • Variable Expressions |
| Copyright Year | 2014 |
| Keywords | definition, integer |